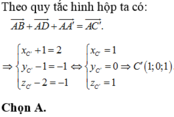Các câu hỏi tương tự
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết tọa độ các đỉnh A(-3;2;1), C(4;2;0), B'(-2;1;1), D'(3;5;4). Tìm tọa độ điểm A’ của hình hộp
A. A'(-3;3;1)
B. A'(-3;-3;3)
C. A'(-3;-3;-3)
D. A'(-3;3;3)
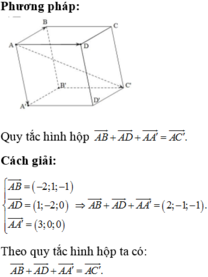
Trong không gian Oxyz cho hình hộp ABCD ABCD. Biết
A
1
;
0
;
1
,
B
2
;
1
;
2
,
D
1
;
−
1
;
1...
Đọc tiếp
Trong không gian Oxyz cho hình hộp ABCD A'B'C'D'. Biết A = 1 ; 0 ; 1 , B = 2 ; 1 ; 2 , D = 1 ; − 1 ; 1 và C ' = 4 ; 5 ; − 5 . Tìm tọa độ đỉnh D'.
A. D ' 5 ; 6 ; − 4
B. D ' − 1 ; − 6 ; 8
C. D ' − 3 ; − 8 ; 6
D. D ' 3 ; 4 ; − 6
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' biết A(2;-1;2), C(-2;3;2), B'(1;2;1), D'(3;0;1). Khi đó tọa độ điểm B là
A. B(-1;2;2)
B. B(1;-2;-2)
C. B(2;-2;1)
D. B(2;-1;2)
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.ABCD biết
A
2
;
−
1
;
2
,
C
−
2
;
3
;
2
,
B
1
;
2
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' biết A 2 ; − 1 ; 2 , C − 2 ; 3 ; 2 , B ' 1 ; 2 ; 1 , D ' 3 ; 0 ; 1 . Khi đó tọa độ điểm B là
A. B(-1;2;2)
B. B(1;-2;-2)
C. B(2;-2;1)
D. B(2;-1;2)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P). A.
3
x
+
2
y
+
z
+
14
0
B.
2
x
+
y
+
3
z
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3 x + 2 y + z + 14 = 0
B. 2 x + y + 3 z + 9 = 0
C. 3 x + 2 y + z - 14 = 0
D. 2 x + y + z - 9 = 0
Trong không gian tọa độ với hệ tọa độ Oxyz, cho ba điểm A(1;2;-1), B(2;-1;3) và C(-3;5;1). Gọi điểm D(a;b;c) thỏa mãn tứ giác ABCD là hình bình hành. Tính tổng T = a + b + c.
A. T = 1.
B. T = 5.
C. T = 3.
D. T = -1.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1;1;2), B(0;1;1), C(1;0;4) và đường thẳng
d
:
x
-
t
y
2
+
t
z
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1;1;2), B(0;1;1), C(1;0;4) và đường thẳng d : x = - t y = 2 + t z = 3 - t Tọa độ giao điểm của mặt phẳng (ABC) và đường thẳng d là
A. (3;-1;6)
B. (-1;3;6)
C. (3;-1;3)
D. (-3;-1;6)
Trong không gian Oxyz, cho
a
→
−
3
;
2
;
1
và điểm
A
4
;
6
;
−
3
. Tìm tọa độ điểm B thỏa mãn
A
B
→
a...
Đọc tiếp
Trong không gian Oxyz, cho a → − 3 ; 2 ; 1 và điểm A 4 ; 6 ; − 3 . Tìm tọa độ điểm B thỏa mãn A B → = a → .
A. 7 ; 4 ; − 4
B. 1 ; 8 ; − 2
C. − 7 ; − 4 ; 4
D. − 1 ; − 8 ; 2
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ
A
B
→
là A.
A
B
→
1
;
-
1
;
1
B.
A
B
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ A B → là
A. A B → = 1 ; - 1 ; 1
B. A B → = 1 ; 1 ; - 3
C. A B → = 3 ; - 3 ; 3
D. A B → = 3 ; - 3 ; - 3