Tính:
a)
\(A =\) \({12 + 32 + 52 + ... + (2n-1) ^ 2}\)
b)
\(B = {13 + 33 + 53 + …+ (2n -1) ^3 }\)
Bài 1: Tính: A=31+33+35+37+...+3111
B=32+34+36+...+3200
C=51+53+55+...+599
D= 52+54+56+...+5100
Bài 2: Chứng minh các phân số sau tối giản với n ϵ N
a) \(\dfrac{2n+1}{n+1}\) b)\(\dfrac{2n+3}{3n+4}\)
Bài 1:
1) \(9A=3^3+3^5+...+3^{113}\)
\(\Rightarrow8A=9A-A=3^3+3^5+...+3^{113}-3-3^3-...-3^{111}=3^{113}-3\)
\(\Rightarrow A=\dfrac{3^{113}-3}{8}\)
2) \(9B=3^4+3^6+...+3^{202}\)
\(\Rightarrow8B=9B-B=3^4+3^6+...+3^{202}-3^2-3^4-...-3^{200}=3^{202}-3^2=3^{202}-9\)
\(\Rightarrow B=\dfrac{3^{202}-9}{8}\)
3) \(25C=5^3+5^5+...+5^{101}\)
\(\Rightarrow24C=25C-C=5^3+5^5+...+5^{101}-5-5^3-...-5^{99}=5^{101}-5\)
\(\Rightarrow C=\dfrac{5^{101}-5}{24}\)
4) \(25D=5^4+5^6+...+5^{102}\)
\(\Rightarrow24D=25D-D=5^4+5^6+...+5^{102}-5^2-5^4-...-5^{100}=5^{102}-25\)
\(\Rightarrow D=\dfrac{5^{102}-25}{24}\)
Bài 2:
a) Gọi d là UCLN(2n+1,n+1)
\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\n+1⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\2n+2⋮d\end{matrix}\right.\)
\(\Rightarrow\left(2n+2\right)-\left(2n+1\right)⋮d\Rightarrow1⋮d\)
Vậy 2n+1 và n+1 là 2 số nguyên tố cùng nhau
\(\Rightarrow\dfrac{2n+1}{n+1}\) là phân số tối giản
b) Gọi d là UCLN(2n+3,3n+4)
\(\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\3n+4⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}6n+9⋮d\\6n+8⋮d\end{matrix}\right.\)
\(\Rightarrow\left(6n+9\right)-\left(6n+8\right)⋮d\Rightarrow1⋮d\)
\(\Rightarrow\dfrac{2n+3}{3n+4}\) là phân số tối giản
(bài này không đơn giản đâu nha (o w o) )
Câu 1:
Biết hai số 3a . 52 . 5b có ƯCLN là 33 . 52 và BCNN là 34. 53.Tìm a và b
Câu 2:Thực hiện phép tính:
a)5/12+3/16 ; b)4/15-2/9
HẾT RỒI!
a)\(...A=\dfrac{2^{50+1}-1}{2-1}=2^{51}-1\)
b) \(...\Rightarrow B=\dfrac{3^{80+1}-1}{3-1}=\dfrac{3^{81}-1}{2}\)
c) \(...\Rightarrow C+1=1+4+4^2+4^3+...+4^{49}\)
\(\Rightarrow C+1=\dfrac{4^{49+1}-1}{4-1}=\dfrac{4^{50}-1}{3}\)
\(\Rightarrow C=\dfrac{4^{50}-1}{3}-1=\dfrac{4^{50}-4}{3}=\dfrac{4\left(4^{49}-1\right)}{3}\)
Tương tự câu d,e,f bạn tự làm nhé
a) 25 - 53 : 52 + 12 : 22
b) 5 [ ( 85 - 35 : 7 ) : 8 + 90 ] - 50
c) 2. [ ( 7 - 33 : 32 ) 22 + 99 ] - 100
d) 27 : 22 + 54 : 53 . 24 - 3 . 25
e) ( 35 . 37 ) : 310 + 5 . 24 - 73 : 7
f) 32 . [ ( 52 - 3 ) : 11 ] - 24 + 2 . 103
g) ( 62007 - 62006 ) : 62006
h) ( 52001 - 52000 ) : 52000
i) ( 72005 + 72004 ) : 72004
j) ( 57 + 75 ) . ( 68 + 86 ) . ( 24 - 42 )
k) ( 57 + 79 ) . ( 54 + 56 ) . ( 33 . 3 - 92 )
l) [ ( 52 . 23) - 72 . 2 ) : 2 ] 6 - 7 . 25
a, A = 1 + 2 + 22 + 23 + ... + 250 =
b, B = 1 + 3 + 32 + 33 + ... 3100 =
c, C = 5 + 52 + 53 + ... 530 =
d, D = 2100 = 299 + 298 - 297 + ... + 22 - 2
a) \(A=1+2+2^2+...+2^{50}\)
\(\Rightarrow2A=2+2^2+...+2^{51}\)
\(\Rightarrow A=2A-A=2+2^2+...+2^{51}-1-2-2^2-...-2^{50}=2^{51}-1\)
b) \(B=1+3+3^2+...+3^{100}\)
\(\Rightarrow3B=3+3^2+...+3^{101}\)
\(\Rightarrow2B=3B-B=3+3^2+...+3^{101}-1-3-3^2-...-3^{100}=3^{101}-1\)
\(\Rightarrow B=\dfrac{3^{101}-1}{2}\)
c) \(C=5+5^2+...+5^{30}\)
\(\Rightarrow5C=5^2+5^3+...+5^{31}\)
\(\Rightarrow4C=5C-C=5^2+5^3+...+5^{31}-5-5^2-...-5^{30}=5^{31}-5\)
\(\Rightarrow C=\dfrac{5^{31}-5}{4}\)
d) \(D=2^{100}-2^{99}+2^{98}-...+2^2-2\)
\(\Rightarrow2D=2^{101}-2^{100}+2^{99}-...+2^3-2^2\)
\(\Rightarrow3D=2D+D=2^{101}-2^{100}+2^{99}-...+2^3-2^2+2^{100}-2^{99}+...+2^2-2=2^{101}-2\)
\(\Rightarrow D=\dfrac{2^{101}-2}{3}\)
Tính tổng sau:
A=2+22+23+...+219+220
B=5+52+53+...+550
C=1+3+32+33+...+3100
\(A=2+2^2+...+2^{20}\)
\(2A=2^2+2^3+...+2^{21}\)
\(2A-A=2^2+2^3+...+2^{21}-2-2^2-...-2^{20}\)
\(A=2^{21}-2\)
___________
\(B=5+5^2+...+5^{50}\)
\(5B=5^2+5^3+...+5^{51}\)
\(5B-B=5^2+5^3+...+5^{51}-5-5^2-...-5^{50}\)
\(4B=5^{51}-5\)
\(B=\dfrac{5^{51}-5}{4}\)
___________
\(C=1+3+3^2+...+3^{100}\)
\(3C=3+3^2+...+3^{101}\)
\(3C-C=3+3^2+...+3^{101}-1-3-3^2-...-3^{100}\)
\(2C=3^{101}-1\)
\(C=\dfrac{3^{101}-1}{2}\)
2A= 2(2+22+23+...+219+220)
2A= 22+23+24+...+220+221
2A-A=(22+23+24+...+220+221)-(2+22+23+...+219+220)
A=221-2
Vậy A=221-2
Làm tương tự nhee
Chứng minh đẳng thức sau ( v ớ i n ∈ N ∗ ) 1 2 + 3 2 + 5 2 + . . . + 2 n - 1 2 = n 4 n 2 - 1 3
Đặt vế trái bằng S n
Với n = 1 vế trái chỉ có một số hạng bằng 1, vế phải bằng 1
Giả sử đã có 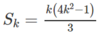 với k ≥ 1. Ta phải chứng minh
với k ≥ 1. Ta phải chứng minh
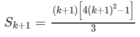
Thật vậy, ta có
S k + 1 = S k + 2 k + 1 - 1 2 = S k + 2 k + 1 2
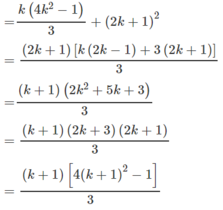
1)Tìm số dư của phép chia B cho 4
B=1+3+32+33+...+3100
2)Thu gọn C=5-52+53-54+...+52023-52024
Bài 1:
$B=1+3+3^2+3^3+...+3^{100}$
$=1+(3+3^2)+(3^3+3^4)+...+(3^{99}+3^{100})$
$=1+3(1+3)+3^3(1+3)+...+3^{99}(1+3)$
$=1+(1+3)(3+3^3+...+3^{99})=1+4(3+3^3+....+3^{99})$
$\Rightarrow B$ chia 4 dư 1.
Bài 2:
$C=5-5^2+5^3-5^4+...+5^{2023}-5^{2024}$
$5C=5^2-5^3+5^4-5^5+...+5^{2024}-5^{2025}$
$\Rightarrow C+5C=5-5^{2025}$
$6C=5-5^{2025}$
$C=\frac{5-5^{2025}}{6}$
tính nhanh:
a,(-25).21.(-2)^2 .(-/-3/).(-1) ^ 2n+1 (nϵN*)
b,(-5)^3.67.(-/-2^3/).(-1)^2n (nϵN*)
c,31.(-18)+31.(-81)-31
d,(-12).47+(-12).52+(-12)
Máy tính đâu,nó sinh ra là để làm gì???