Chứng minh rằng: nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có bán bán kính là AB.

Những câu hỏi liên quan
Bài 1:a/ Cho hình vuông ABCD có cạnh 5cm. Chứng minh rằng: A, B, C, D cùng nằm trên một đường tròn, tính bán kính.b/ Cho hình chữ nhật ABDE có AB 8, BD 6. Chứng minh rằng: A, B, D, E cùng nằm trên một đường tròn, tính bán kính.Bài 2: Cho tam giác ABC, vẽ đường tròn tâm O đường kính BC. (O) cắt AB, AC lần lượt tại D và E, BE giao CD tại K.a/ CMR: CD ^ AB, BE ^ AC.b/ CMR: AK ^ BC.Bài 3: Cho tam giác ABC vuông ở B, AB 8cm, BC 6cm. Gọi D là điểm đối xứng của điểm B qua AC.a. CMR: 4 điểm A, B, C,...
Đọc tiếp
Bài 1:
a/ Cho hình vuông ABCD có cạnh 5cm. Chứng minh rằng: A, B, C, D cùng nằm trên một đường tròn, tính bán kính.
b/ Cho hình chữ nhật ABDE có AB = 8, BD = 6. Chứng minh rằng: A, B, D, E cùng nằm trên một đường tròn, tính bán kính.
Bài 2: Cho tam giác ABC, vẽ đường tròn tâm O đường kính BC. (O) cắt AB, AC lần lượt tại D và E, BE giao CD tại K.
a/ CMR: CD ^ AB, BE ^ AC.
b/ CMR: AK ^ BC.
Bài 3: Cho tam giác ABC vuông ở B, AB = 8cm, BC = 6cm. Gọi D là điểm đối xứng của điểm B qua AC.
a. CMR: 4 điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
b. Vẽ đường kính BE của đường tròn ngoại tiếp tam giác ABC. Chứng minh tứ giác ACDE là hinh thang cân.
Các câu sau đúng hay sai?
a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)
b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C (h.89).
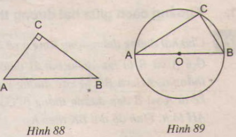
a) Đúng
Gọi O là trung điểm của AB.
Ta có CO là trung tuyến ứng với cạnh huyền nên
⇒ OC = AB/2 = OA = OB.
⇒ A, B, C cùng thuộc đường tròn bán kính OA.
Tâm O là trung điểm của AB nên AB là đường kính.
Vậy C thuộc đường tròn đường kính AB.
b) Đúng
Gọi O là tâm đường tròn.
⇒ OA = OB = OC = R
AB là đường kính nên AB = 2R.
Tam giác ABC có CO là trung tuyến và CO = AB/2
⇒ ΔABC vuông tại C.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi R là bán kính của đường tròn ngoại tiếp. r là bán kính của đường tròn nội tiếp tam giác ABC. Chứng minh rằng: AB + AC = 2(R + r)

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.
Ta có: BC = 2R
Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F
Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.
Suy ra: AD = AE = EO = OD = r
Theo tính chất hai tiếp tuyến cắt nhau ta có:
AD = AE
BD = BF
CE = CF
Ta có: 2R + 2r = BF + FC + AD + AE
= (BD + AD) + (AE + CE)
= AB + AC
Vậy AB = AC = 2(R + r)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB > AC), có đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường tròn (C) tại điểm thứ hai D
a) chứng minh BC là đường trung trực của AD
b) Chứng minh BD là tiếp tuyến của đường tròn (C).
Tam giác ABC nhọn (AB AC)Kẻ các đoạn BE, CF cắt nhau tại Ha. Chứng minh 4 điểm B, C, E, F thuộc 1 đường tròn, xác định tâm và bán kính đường tròn đób. Chứng minh 4 điểm A, F, H, E thuộc 1 đường tròn, xác định tâm và bán kính đường tròn đóc. Chứng minh AF.AB AE.AC và góc AFE góc ACBd. Kéo dài AH cắt BC tại M. Chứng minh AM vuông BCe. Chứng minh 4 điểm M, H, E, C và 4 điểm M, H, F, B cùng 1 đường tròn
Đọc tiếp
Tam giác ABC nhọn (AB < AC)
Kẻ các đoạn BE, CF cắt nhau tại H
a. Chứng minh 4 điểm B, C, E, F thuộc 1 đường tròn, xác định tâm và bán kính đường tròn đó
b. Chứng minh 4 điểm A, F, H, E thuộc 1 đường tròn, xác định tâm và bán kính đường tròn đó
c. Chứng minh AF.AB = AE.AC và góc AFE = góc ACB
d. Kéo dài AH cắt BC tại M. Chứng minh AM vuông BC
e. Chứng minh 4 điểm M, H, E, C và 4 điểm M, H, F, B cùng 1 đường tròn
Câu 5. (3,5 điểm) Cho tam giác ABC (AB AC) có ba góc nhọn nội tiếp trong đường tròntâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.a) Chứng minh rằng 4 điểm A, E, H, F cùng thuộc một đường trònb) Vẽ đường kính AK của đường tròn (O). Chứng minh tam giác ABD và tam giác AKCđồng dạng với nhau. Suy ra AB.AC 2R.AD.c) Chứng minh rằng OC vuông góc với DE
Đọc tiếp
Câu 5. (3,5 điểm) Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp trong đường tròn
tâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.
a) Chứng minh rằng 4 điểm A, E, H, F cùng thuộc một đường tròn
b) Vẽ đường kính AK của đường tròn (O). Chứng minh tam giác ABD và tam giác AKC
đồng dạng với nhau. Suy ra AB.AC = 2R.AD.
c) Chứng minh rằng OC vuông góc với DE
tam giác ABC vuông tại A, M là trung điểm BC
a)Chứng minh A,B,C thuộc đường tròn (M)
b)Biết AB=6cm, AC=8cm.Tính bán kình đường tròn ngoại tiếp tam giác ABC
a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
=>ΔABC nội tiếp (M)
b: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}=5\left(cm\right)\)
=>R=5cm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB 4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D
Cho tam giác ABC vuông tại A có AB4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D.
a) Tính độ dài đoạn thẳng AH
b) Chứng minh BD là tiếp tuyến của đường tròn (C)
c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua...
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D Cho tam giác ABC vuông tại A có AB=4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D. a) Tính độ dài đoạn thẳng AH b) Chứng minh BD là tiếp tuyến của đường tròn (C) c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB,BD lần lượt tại P,Q. Chứng minh EF bình phương =4PE.QF
a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
AH=4*3/5=2,4cm
b: ΔCAD cân tại C
mà CH là đường cao
nên CH là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
Do dó: ΔCAB=ΔCDB
=>góc CDB=90 độ
=>BD là tiếp tuyến của (C)
Đúng 0
Bình luận (0)
cho đường tròn O đường kính AA'=2R.một dây cung BC vuông góc bán kính OA' tại trung điểm H của OA' a)chứng minh rằng tam giác OBA' và tam giác ABC là các tam giác đều.Tính cạnh tam giác ABC b)đường BO cắt đường tròn O tại D đường DH cắt đường tròn tại M.Tính DH;DM c)tính diện tích tam giác HMC
a:
góc ABA'=góc ACA'=1/2*180=90 độ
Xét ΔBOA' có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBOA' cân tại B
mà OB=OA'
nên ΔBOA' đều
=>góc A'BH=30 độ
=>góc ABC=60 độ
Xét ΔACB có
AH vừa là đường cao, vừa là trung tuyến
góc ABC=60 độ
=>ΔACb đều
b: ΔOBA' đều có BH là đường cao
nên BH=OA'*căn 3/2=R*căn 3/2
=>CH=R*căn 3/2
=>BC=R*căn 3
=>DC=căn DB^2-BC^2=R
DH=căn DC^2+CH^2=R*căn 7/2
Đúng 0
Bình luận (0)















