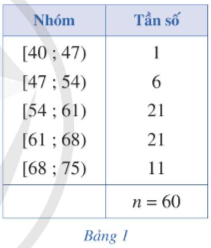
Tính khoảng biến thiên của mẫu số liệu ghép nhóm cho bởi Bảng 1 trong phần mở đầu.
Với mẫu số liệu ghép nhóm cho trong HĐ2, hãy cho biết tứ phân vị nhất \({Q_1}\) và tứ phân vị thứ ba \({Q_3}\) thuộc nhóm nào.
Cho mẫu số liệu ghép nhóm như Bảng 3.2
Cỡ mẫu là: \(n = 21\).
Suy ra tứ phân vị thứ nhất \({Q_1}\)là \(\frac{{{x_5} + {x_6}}}{2}\). Do \({x_5};{x_6}\) đều thuộc nhóm [5;10) nên từ phân vị thứ nhất thuộc nhóm [5;10).
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{16}} + {x_{17}}}}{2}\) . Do \({x_{16}};\;{x_{17}}\)đều thuộc nhóm [10; 15) nên tứ phân vị thứ ba thuộc nhóm [10; 15).
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)
Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:
163 159 172 167 165 168 170 161
Tính khoảng biến thiên của mẫu số liệu này.
Số lớn nhất là 172, số nhỏ nhất là 159
R = 172 - 159 = 13
Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilomet) của 40 chiếc ô tô:

a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy với năm nhóm ứng với năm nửa khoảng: [100 ; 120), [120 ; 140), [140 ; 160), [160 ; 180), [180 ; 200)
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
c) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?
a, Bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
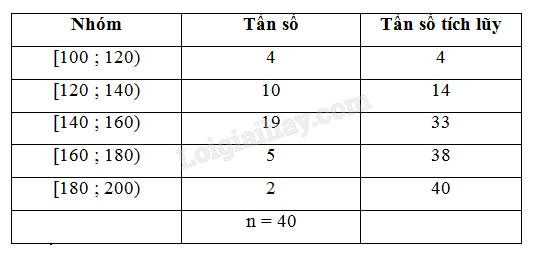
b, - Trung bình cộng là:
\(\overline{x}=\dfrac{110\cdot4+130\cdot15+150\cdot14+170\cdot5+190\cdot2}{40}=143\)
- Trung vị là: \(M_e=140+\left(\dfrac{20-19}{14}\right)\cdot20\simeq141\)
- \(Q_1=120+\left(\dfrac{10-4}{15}\right)\cdot20\simeq128\\ Q_2=M_e\simeq141\\ Q_3=140+\left(\dfrac{30-19}{15}\right)\cdot20=155,6\)
c, Mốt của mẫu số liệu là:
Có nhóm 2 là nhóm có tần số lớn nhất
\(\Rightarrow M_o=120+\left(\dfrac{15-4}{2\cdot15-4-14}\right)\cdot20\simeq138,3\)
Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):
2,977 3,155 3,920 3,412 4,236
2,593 3,270 3,813 4,042 3,387
Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu này.
Sắp xếp theo thứ tự không giảm.
2,593 2,977 3,155 3,270 3,387 3,412 3,813 3,920 4,042 4,236
Khoảng biến thiên \(R = 4,236 - 2,593 = 1,643\)
Vì n=10 nên ta có:
\({Q_1} = 3,155\); \({Q_3} = 3,920\)
Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1} = 3,920 - 3,155\)\( = 0,765\)
\(\overline x \approx 3,481\)
Ta có:
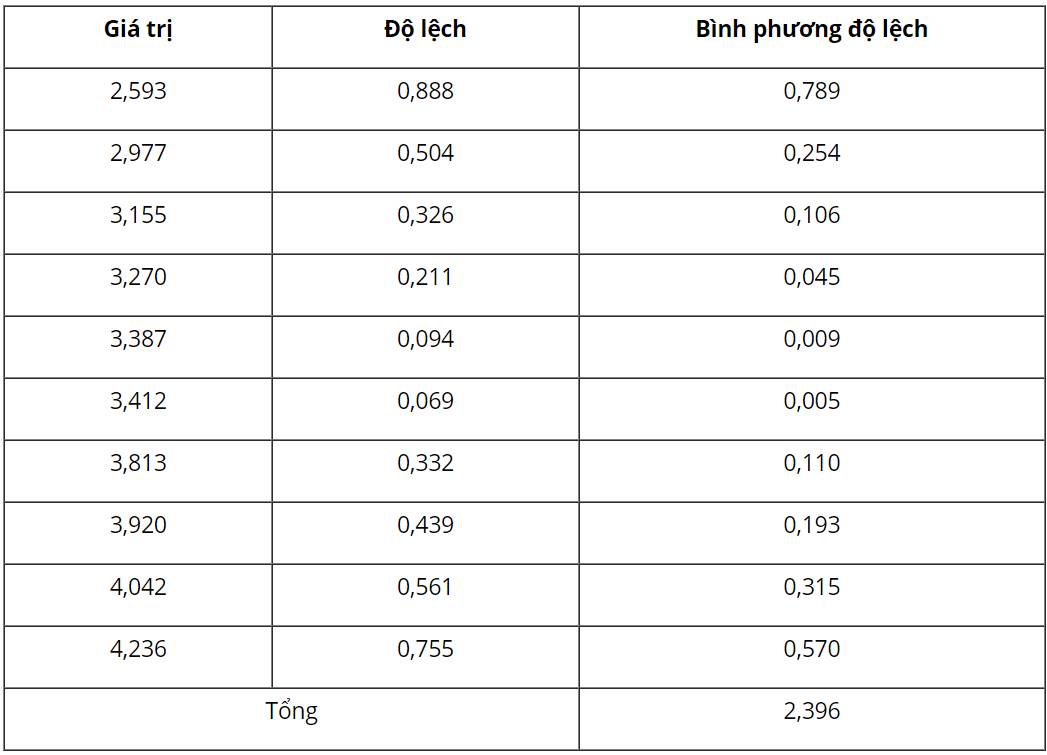
Độ lệch chuẩn: \(s = \sqrt {0,2396} \approx 0,489\)Phương sai là: \({s_2} = \frac{{2,396}}{{10}} = 0,2396\)
Khảo sát thời gian tự học của các học sinh trong lớp theo mẫu bên.

a) Hãy lập bảng thống kê cho mẫu số liệu ghép nhóm thu được
b) Có thể tính chính xác thời gian tự học trung bình của các học sinh trong lớp không?
c) Có cách nào tính gần đúng thời gian tự học trung bình của các học sinh trong lớp dựa trên mẫu số liệu ghép nhóm này không?
Tham khảo:
a)

b) Không thể tính chính xác, chúng ta chỉ có thể tinh số gần đúng thời gian tự học trung bình của các học sinh trong lớp
c) Giá trị đại diện của nhóm bằng trung bình giá trị đầu mút phải và trái của nhóm đó
Nhóm \( \ge 4.5\) là nhóm mở nên ta dựa theo nhóm gần đó nhất là nhóm [3;4.5) để lấy giá trị đại diện

Số trung binh của mẫu số liệu: : \(\bar x = \frac{{0.75 \times 8 + 2.25 \times 23 + 2.75 \times 6 + 5.25 \times 3}}{{40}} = 2.25\).
Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.
a) Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.
b) Tìm khoảng biến thiên của mẫu số liệu đó.
c) Tìm khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
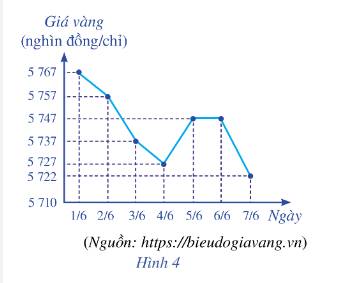
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5767 5757 5737 5727 5747 5747 5722
b) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 5767 - 5722 = 45\)
c) +) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5722 5727 5737 5747 5747 5757 5767
+) Các tứ phân vị của mẫu số liệu là:
Trung vị của mẫu số liệu: \({Q_2}\) = 5747.
Trung vị của dãy 5722 5727 5737 là: \({Q_1}\) = 5727.
Trung vị của dãy 5747 5757 5767 là: \({Q_3}\) = 5757.
+) Khoảng tứ phân vị của mẫu số liệu là: \({\Delta _Q} ={Q_3} - {Q_1}\) = 5757- 5727= 30.
d) +) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là: \(\overline x = \frac{{5722{\rm{ + }}5727{\rm{ + }}5737{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5757{\rm{ + }}5767}}{7} = 5743,43\) ( nghìn đồng/ chỉ)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5722 - \overline x } \right)}^2} + {{\left( {5727 - \overline x } \right)}^2} + ... + {{\left( {5767 - \overline x } \right)}^2}} \right]}}{7} \approx 219,39\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} = \sqrt {219,39} \approx 14,81\)( nghìn đồng/ chỉ)
Một phòng khám thống kê số bệnh nhân đến khám bệnh mỗi ngày trong tháng 4 năm 2022 ở bảng sau:

a) Hãy ước lượng các tử phân vị của mẫu số liệu ghép nhóm trên.
b) Quản lí phòng khám cho rằng có khoảng 25% số ngày khám có nhiều hơn 35 bệnh nhân đến khám. Nhận định trên có hợp lí không?
a) Do số bệnh nhân là số nguyên nên ta hiệu chỉnh như sau:

Số bệnh nhân đến khám bệnh mỗi ngày trong tháng 4 năm 2022 là:
\(n = 7 + 8 + 7 + 6 + 2 = 30\).
Gọi \({x_1};{x_2};...;{x_{30}}\) là số bệnh nhân đến khám bệnh mỗi ngày được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_7} \in \begin{array}{*{20}{l}}{\left[ {0,5;10,5} \right)}\end{array};{x_8},...,{x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array};{x_{16}},...,{x_{22}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array};\\{x_{23}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{l}}{\left[ {40,5;50,5} \right)}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\)
Do \({x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array},{x_{16}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 20,5\).
• Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 30;{n_m} = 8;C = 7;{u_m} = 10,5;{u_{m + 1}} = 20,5\)
Do \({x_8} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{30}}{4} - 7}}{8}.\left( {20,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \({x_{23}}\).
Ta có: \(n = 30;{n_j} = 6;C = 7 + 8 + 7 = 22;{u_j} = 30,5;{u_{j + 1}} = 40,5\)
Do \({x_{23}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 30,5 + \frac{{\frac{{3.30}}{4} - 22}}{6}.\left( {40,5 - 30,5} \right) \approx 31,3\)
b) Do \({Q_3} \approx 31,3\) nên nhận định trên hợp lí.
Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau:

a) Hiệu chỉnh để thu được mẫu số liệu ghép nhóm dạng Bảng 3.2.
b) Tìm các tứ phân vị và giải thích ý nghĩa của chúng.
Tham khảo:
a)

b) Cỡ mẫu \(n = 60\)
Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{15}} + {x_{16}}}}{2}\). Do \({x_{15}},\;{x_{16}}\) đều thuộc nhóm \(\left[ {40;50} \right)\) nên nhóm náy chứa \({Q_1}\). Do đó,
\(p = 5;\;\;{a_5} = 40;\;\;{m_5} = 15;\;\;{m_1} + {m_2} + {m_3} + {m_4} = 1 + 2 + 4 + 6 = 13;\;{a_6} - {a_5} = 10\)
Ta có \({Q_1} = 40 + \frac{{\frac{{60}}{4} - 13}}{{15}} \times 10 = 41,33\)
Ý nghĩa: Có 25% số giá trị nhỏ hơn 41,33
Tứ phân vị thứ hai, \({M_e}\) là \(\frac{{{x_{30}} + {x_{31}}}}{2}\). Do \({x_{30}};\;{x_{31}}\) đều thuộc nhóm \(\left[ {50;60} \right)\) nên nhóm này chứa \({M_e}\). Do đó,
\(p = 6;\;\;{a_6} = 50;\;\;{m_6} = 12;\;\;{m_1} + {m_2} + {m_3} + {m_4} + {m_5} = 1 + 2 + 4 + 6 + 15 = 13;\;{a_7} - {a_6} = 10\)
Ta có: \({Q_2} = 50 + \frac{{\frac{{60}}{2} - 28}}{{12}} \times 10 = 51,66\)
Ý nghĩa: Có 50% số giá trị nhỏ hơn 51,66
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{45}} + {x_{46}}}}{2}\). Do \({x_{45}},\;{x_{46}}\) đều thuộc nhóm \(\left[ {60;70} \right)\) nên nhóm náy chứa \({Q_3}\). Do đó,
\(p = 7;\;\;{a_7} = 60;\;\;{m_7} = 10;\;\;{m_1} + {m_2} + {m_3} + {m_4} + {m_5} + {m_6} = 1 + 2 + 4 + 6 + 15 + 12 = 40; {a_8} - {a_7} = 10\).
Ta có: \({Q_3} = 60 + \frac{{\frac{{60 \times 3}}{4} - 40}}{{10}} \times 10 = 65\)
Ý nghĩa: Có 75% số giá trị nhỏ hơn 65.
Cho hai biểu đồ chấm điểm biểu diễn hai mẫu số liệu A, B như sau:
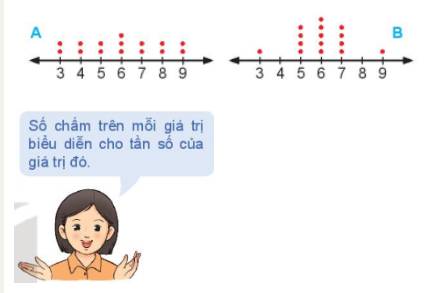
Không tính toán, hãy cho biết:
a) Hai mẫu số liệu này có cùng khoảng biến thiên và số trung bình không?
b) Mẫu số liệu nào có phương sai lớn hơn?
a) Cả 2 mẫu đều có n=15.
Ta có cả 2 mẫu đều có giá trị nhỏ nhất là 3, giá trị lớn nhất là 9
Do đó cả 2 mẫu cùng khoảng biến thiên.
Cả 2 biểu đồ này có dạng đối xứng nên giá trị trung bình của hai mẫu A và B bằng nhau.
b) Từ biểu đồ ta thấy, mẫu A có các số liệu đồng đều và ổn định hơn mẫu B nên phương sai của mẫu A nhỏ hơn mẫu B.