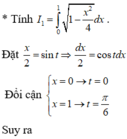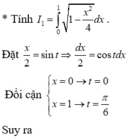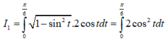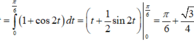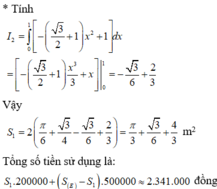giuspmifnh b1 với

Những câu hỏi liên quan
Chứng minh bất đẳng thức :
\(\sin\frac{x+y}{2}\ge\frac{1}{2}\left(\sin x+\sin y\right)\) với 0 < x,y ,180
Giuspmifnh với nhá !!!
Giả sử cần tính tách giá trị trong các ô A1 và B1, sau đó cộng với giá trị trong ô C3. Công thức nào đúng?
A. = A1*B1+C3
B. = (A1*B1)+C3
C. = A1*(B1+C3)
D. = A1.B1+C3
Xem thêm câu trả lời
Câu 16: Giả sử cần tính tổng giá trị các ô A1 và C1, sau đó nhân với giá trị trong ô B1. Công thức nào sau đây là đúng?
A. = A1+C1*B1 B. (A1+C1)*B1 C. = (A1+C1)*B1 D. = (A1+C1)B1
Xem thêm câu trả lời
Với A1=10, A2=30, A3=20, B1=20, B2=40, B3=50, B4=100
Tính kết quả:
a) = AVERAGE(SUM(B1, B2, B3)
b) = SUM(A1, B1, B4)
c) = MAX(A1, B1, B4)
d) = SUM( AVERAGE(B1:B4)
a) \(\approx\) 36,6
b) 130
c) 100
Đúng 0
Bình luận (0)
MN ơi giải giúp em bài này với : a) chứng tỏ tia A3=B1 b) chứng tỏ A3 + B4= 180 độ c) chứng tỏ A1=B1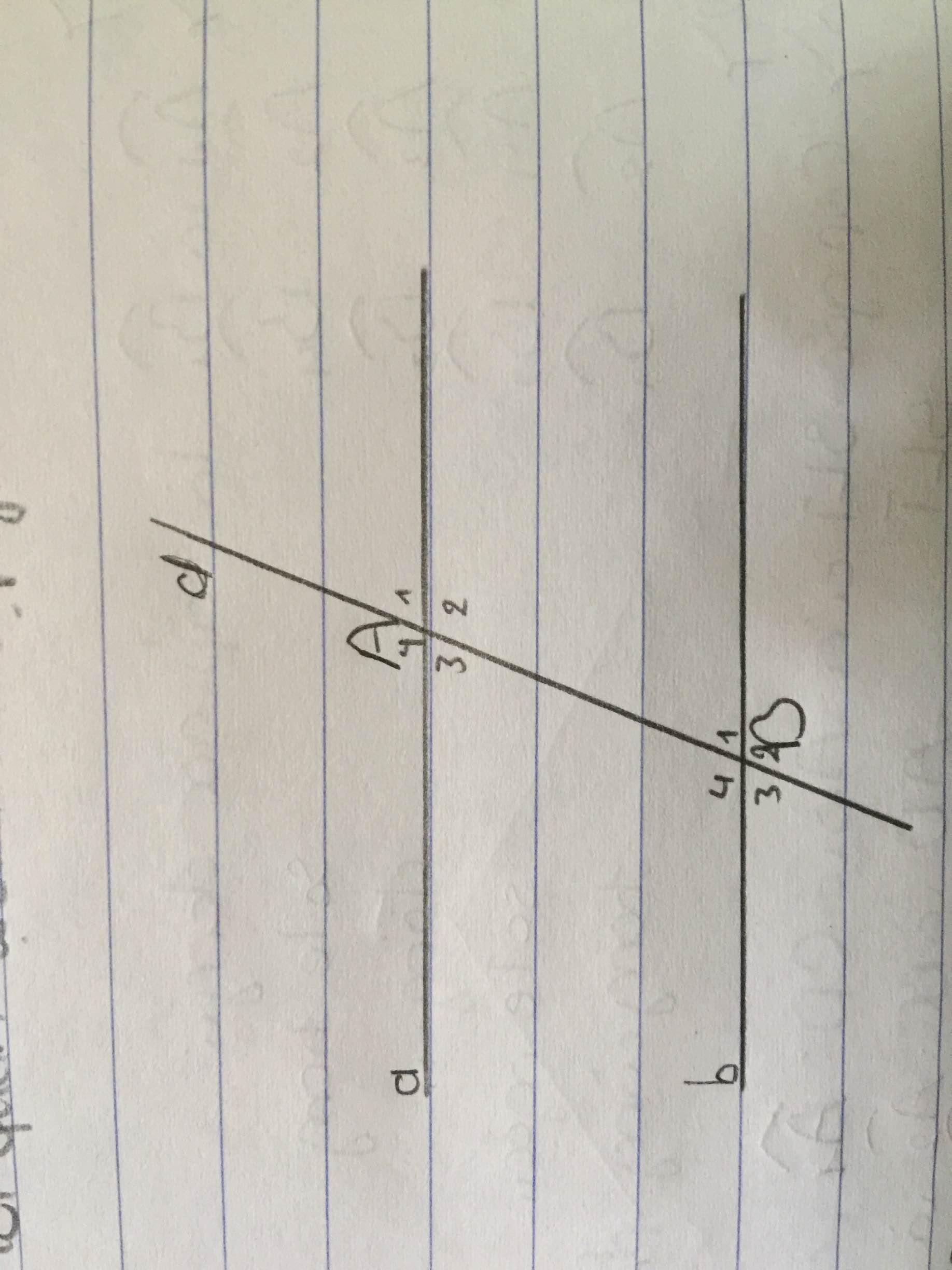
a)A3=B1 vì // ( sole trong = nhau) nhớ tick nhé
Đúng 0
Bình luận (0)
b) vì // (trong cùng phía bù nhau)
nhớ tick nhé
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
=(A1+B1)/B1 kết quả
=(A1*B1)/B1^B1
=(A1/B1)^2
=(A1^B1)^B1

giúp mình b1 với
1 Linh said that her uncle had worked in Hai Phong for 10 years
2 She told us that she was having dinner with Rachel the following day
3 The teacher said to the children that they must wash their hands
4 Susan said that they hadn't left for London at 5 p.m the day before
5 Tom said to me that his brother would stay there the following Friday
6 He wanted to know when the train left
7 Jack asked the old man how long he had worked in that company
8 My parents asked me what time your friend would arrive that weekend
9 They asked Mr. Quang if he had seen a UFO the evening before
10 The boy askes->asked Anna if he might use her phone
\(\text{#♪◈₰♣}\)
Đúng 5
Bình luận (2)
cho giá trị A1=5;B1=8.Hãy chọn kết quả của công thức=A1*2+B1*3
A.24
B.18
C.13
D.34
MN GIẢI THÍCH RA GIÚP VỚI Ạ
cho giá trị A1=5;B1=8.Hãy chọn kết quả của công thức=A1*2+B1*3
A.24
B.18
C.13
D.34
Đúng 3
Bình luận (1)
giúp mình B1 với ạ 
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=BH\cdot CH\)
\(\Leftrightarrow x=\dfrac{6^2}{12}=\dfrac{36}{12}=3\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow y^2=3^2+6^2=9+36=45\)
hay \(y=3\sqrt{5}\left(cm\right)\)
b) Ta có: \(\sin^2\widehat{A}+\cos^2\widehat{A}=1\)
\(\Leftrightarrow\cos^2\widehat{A}=\dfrac{3}{4}\)
hay \(\cos\widehat{A}=\dfrac{\sqrt{3}}{2}\)
Ta có: \(\tan\widehat{A}=\dfrac{\sin\widehat{A}}{\cos\widehat{A}}\)
\(=\dfrac{1}{2}:\dfrac{\sqrt{3}}{2}\)
\(=\dfrac{\sqrt{3}}{3}\)
Đúng 1
Bình luận (0)
Lời giải:
a. Theo định lý Pitago cho tam giác $ABH$:
$y^2=36+x^2(1)$
Theo hệ thức lượng trong tam giác vuông:
$y^2=x(x+12)(2)$
Từ $(1);(2)\Rightarrow x^2+36=x(x+12)$
$36=12x$
$x=3$ (cm)
$y^2=3(3+12)=45\Rightarrow y=3\sqrt{5}=6,708$ (cm)
b.
Giả sử $a = \widehat{B}$
$\cos a=\cos B=\frac{AB}{BC}=\frac{1}{2}$
$\Rightarrow AB=\frac{BC}{2}$
Theo Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{BC^2-(\frac{BC}{2})^2}=\frac{\sqrt{3}}{2}BC$
$\sin a= \sin B=\frac{AC}{BC}=\frac{\sqrt{3}}{2}$
$\tan a=\tan B=\frac{AC}{AB}=\frac{\frac{BC}{2}}{\frac{\sqrt{3}}{2}BC}=\frac{\sqrt{3}}{3}$
Đúng 1
Bình luận (0)
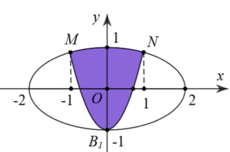
Một biển quảng cáo có dạng hình elip với bốn đỉnh
A
1
,
A
2
,
B
1
,
B
2
như hình vẽ bên. Người ta chia elip bởi parabol có đỉnh
B
1
, trục đối xứng
B
1
,
B
2
và đi qua các điểm M...
Đọc tiếp
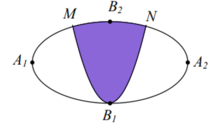
Một biển quảng cáo có dạng hình elip với bốn đỉnh A 1 , A 2 , B 1 , B 2 như hình vẽ bên. Người ta chia elip bởi parabol có đỉnh B 1 , trục đối xứng B 1 , B 2 và đi qua các điểm M, N. Sau đó sơn phần tô đậm với giá 200.000 đồng/ m2 và trang trí đen led phần còn lại với giá 500.000 đồng/ m2 . Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng A 1 A 2 = 4 m , B 1 B 2 = 2 m , M N = 2 m .
A. 2.341.000 đồng
B. 2.057.000 đồng
C. 2.760.000 đồng
D. 1.664.000 đồng