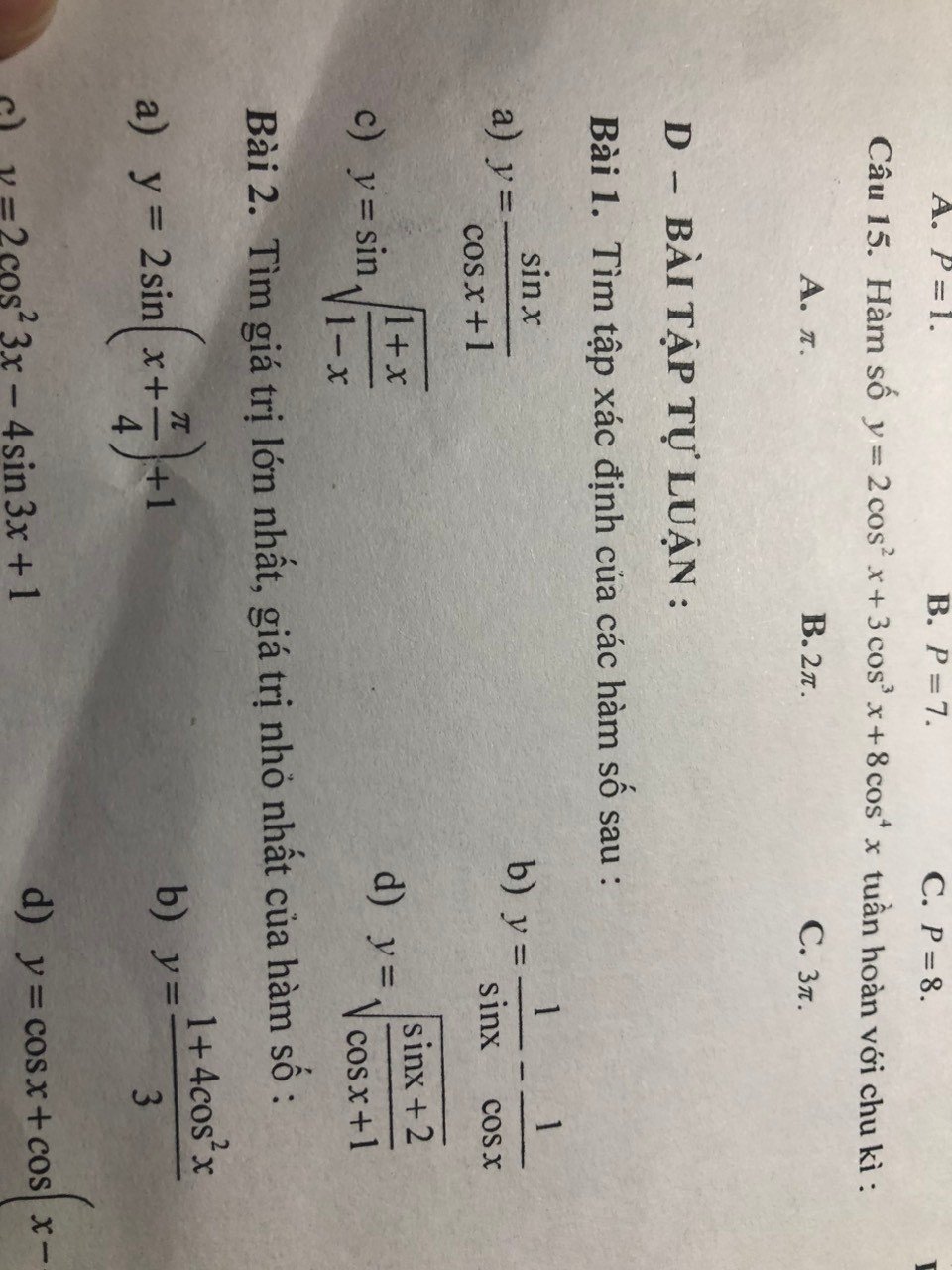Bài 1:
a: ĐKXĐ: \(cosx+1\ne0\)
=>\(cosx\ne-1\)
=>\(x\ne\Omega+k2\Omega\)
b: ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\end{matrix}\right.\)
=>\(sin2x\ne0\)
=>\(2x\ne k\Omega\)
=>\(x\ne\dfrac{k\Omega}{2}\)
c: ĐKXĐ: \(\dfrac{1+x}{1-x}>=0\)
=>\(\dfrac{x+1}{x-1}< =0\)
=>-1<=x<1
d: \(\left\{{}\begin{matrix}-1< =sinx< =1\\-1< =cosx< =1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-1+2< =sinx+2< =1+2\\-1+1< =cosx+1< =1+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1< =sinx+2< =3\\0< =cosx+1< =2\end{matrix}\right.\)
=>\(sinx+2>=0\forall x;cosx+1>=0\forall x\)
Để hàm số \(\sqrt{\dfrac{sinx+2}{cosx+1}}\) xác định thì \(\dfrac{sinx+2}{cosx+1}>=0\)
=>\(cosx+1< >0\)
=>\(cosx\ne-1\)
=>\(x\ne\Omega+k2\Omega\)