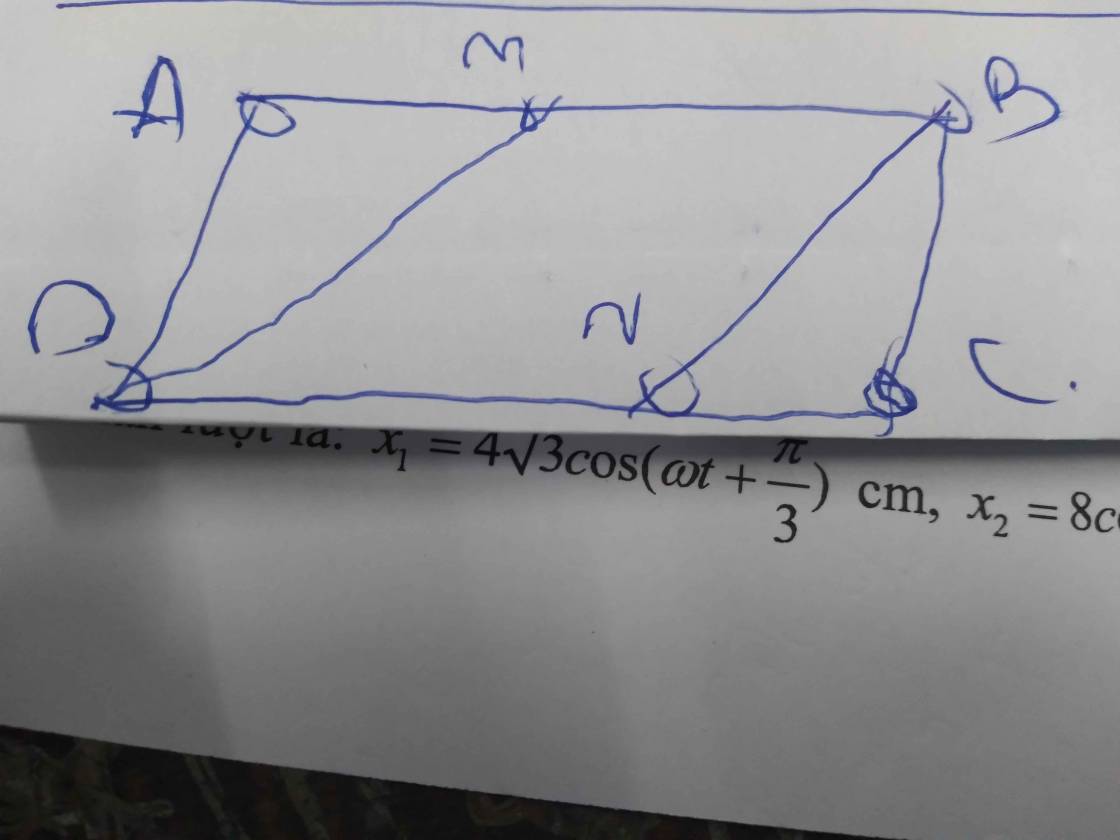
Cho hình bình hành ABCD có góc B>90 độ.Tia phân giác của góc A cắt CD tại E.Tia phân giác của góc C cắt AB tại F.CM AECF là hình bình hành

Những câu hỏi liên quan
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F. CMR:
a) DE // BF
b) Tứ giác DEBF là hình gì?
c) Tam giác ADE = Tam giác CBF
d) C/m: Tứ giác AECF là hình bình hành
e) AC, DB, EF đồng quy
a: Ta có: \(\widehat{ADE}=\dfrac{\widehat{ADC}}{2}\)
\(\widehat{CBF}=\dfrac{\widehat{CBA}}{2}\)
mà \(\widehat{ADC}=\widehat{CBA}\)
nên \(\widehat{ADE}=\widehat{CBF}\)
Xét ΔADE và ΔCBF có
\(\widehat{ADE}=\widehat{CBF}\)
AD=BC
\(\widehat{DAE}=\widehat{BCF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
Ta có: AE+EB=AB
CF+DF=CD
mà AB=CD
và AE=CF
nên EB=DF
Xét tứ giác DEBF có
EB//DF
EB=DF
Do đó: DEBF là hình bình hành
Suy ra: DE//BF
d: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Đúng 1
Bình luận (0)
e: Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường\(\left(1\right)\)
Ta có: EBFD là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra AC,BD,EF đồng quy
Đúng 1
Bình luận (0)
Bài 2: cho hình bình hành ABCD có AB>BC, phân giác của góc D cắt AB tại M,phân giác của góc B cắt CD tại N.c/m
a,AM=CN
b,tứ giác DMBN là hình bình hành
cho hình bình hành abcd có ab>bc . đường phân giác của góc d cắt ab tại m đường phân giác góc b cắt cd tại n
a, chuwnngs minh am =cn
b, chưng minh tú giác dmbc là hình bình hành
Cho hình bình hành ABCD có đường chéo BD tại M , cắt CD tại E . Từ C kẻ đường thẳng vuông góc BD tại N , cắt AB tại F. Chứng minh rằng : a) tam giác AMD = tam giác CNB b) tứ giác AMCN là hình bình hành c) tứ giác AECF là hình bình hành ( CÓ HÌNH VẼ) GIÚP EM VỚI Ạ EM ĐANG CẦN GẤP
Cho hình bình hành ABCD có AB<CD. Phân giác góc A cắt BC tại I, phần giác góc C cắt AD tại K. Chứng minh rằng AICK là hình bình hành.
Cho hình bình hành ABCD . tia phân giác góc B cắt DC tại M , Tia phân giác Của góc D cắt AB tại N: a) chứng minh Tam giác ADN = tam giác CBM b) C/m tứ giác DMBN là hình bình hành c) C/m tức giác AMCN là hình bình hành
a: Xét ΔADN và ΔCBM có
góc A=góc C
AD=CB
góc ADN=góc CBM
=>ΔADN=ΔCBM
b: ΔADN=ΔCBM
=>AN=CM
AN+NB=AB
CM+MD=CD
mà AN=CM và AB=CD
nên NB=MD
mà NB//MD
nên NBMD là hình bình hành
c: Xét tứ giác AMCN có
AN//CM
AN=CM
=>AMCN là hình bình hành
Đúng 0
Bình luận (0)
Cho Hình Bình Hành ABCD tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt Cd tại F. c/m a) tam giác ADE tam giác CBF b) Tứ giác DEBF là HBH c) Tính góc DEB biết góc A 120 độ
Đọc tiếp
Cho Hình Bình Hành ABCD tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt Cd tại F. c/m a) tam giác ADE = tam giác CBF b) Tứ giác DEBF là HBH c) Tính góc DEB biết góc A = 120 độ
a: Xét ΔADE và ΔCBF có
góc A=góc C
AD=CB
góc ADE=góc CBF
=>ΔADE=ΔCBF
b: ΔADE=ΔCBF
=>góc AED=góc CFB
=>góc AED=góc FBE
=>DE//BF
Xét tứ giác BEDF có
BE//DF
DE//BF
=>BEDF là hình bình hành
c: góc AED=góc EDC
góc EDC=góc ADE
=>góc AED=góc ADE
=>ΔADE cân tại A
=>góc AED=góc ADE=(180-120)/2=30 độ
góc DEB=180-30=150 độ
Đúng 1
Bình luận (0)
Cho hình bình hành \(ABCD\) (\(AB > BC\)). Tia phân giác của góc \(D\) cắt \(AB\) tại \(E\), tia phân giác của góc \(B\) cắt \(CD\) tại \(F\)
a) Chứng minh \(DE\) // \(BF\)
b) Tứ giác \(DEBF\) là hình gì?
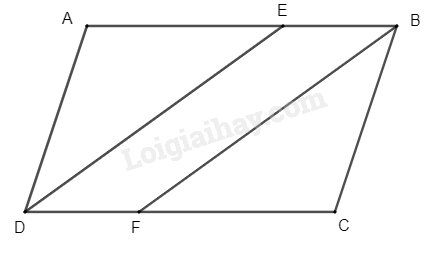
a) Vì \(DE\), \(BF\) là phân giác (gt)
Suy ra \(\widehat {{\rm{ADE}}} = \widehat {{\rm{EDC}}} = \frac{{\widehat {ADC}}}{2}\); \(\widehat {{\rm{EBF}}} = \widehat {{\rm{CBF}}} = \frac{{\widehat {ABC}}}{2}\) (1)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AB\) // \(CD\) và \(\widehat {ADC} = \widehat {ABC}\) (2)
Suy ra \(\widehat {{\rm{AED}}} = \widehat {{\rm{EDC}}}\) (so le trong) (3)
Từ (1), (2), (3) suy ra \(\widehat {AED} = \widehat {ABF}\)
Mà hai góc ở vị trí đồng vị
Suy ra \(DE\) // \(BF\)
b) Xét tứ giác \(DEBF\) ta có:
\(DE\) // \(BF\) (cmt)
\(BE\) // \(DF\) (do \(AB\) // \(CD\))
Suy ra \(DEBF\) là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Phân giác D cắt AB ở E
a) Cm AD=AE và góc AED=góc B/2
b)P/giác góc B cắt CD tại F.Cm DEBF là hbh
c)Nếu AB=AD. N/ X về p/giác góc B và D