Bài 1: Không làm tính chia, hãy tính số dư trong phép chia
\(a,\left(x^4-6x^2+2x+28\right):\left(x-1\right)\)
\(b,\left(x^4-6x^2+2x+28\right):\left(x-2\right)\)

Những câu hỏi liên quan
Làm phép chia bằng cách áp dụng hằng đẳng thức:
a) \(\left(x^8-2x^4y^4+y^8\right):\left(x^2+y^2\right)\)
b) \(\left(64x^3+27\right):\left(16x^2-12x+9\right)\)
c) \(\left(x^3-9x^2+27x-27\right):\left(x^2-6x+9\right)\)
d) \(\left(x^3y^6z^9-1\right):\left(xy^2z^3-1\right)\)
a: \(=\dfrac{\left(x^4-y^4\right)^2}{x^2+y^2}=\left(x^2-y^2\right)^2\cdot\left(x^2+y^2\right)\)
b: \(=\dfrac{\left(4x+3\right)\left(16x^2-12x+9\right)}{16x^2-12x+9}=4x+3\)
Đúng 0
Bình luận (1)
Tính nhanh :
a) \(\left(x+2\right)^3-x\left(x^2+6x-5\right)-8\)
b) \(\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)+3x^2-2x\)
c) \(\left(2x+1\right)\left(4x^2+2x+1\right)-8x\left(x^2+1\right)-5\)
Nhanh nhé ! Ai nhanh và đúng nhất mình tick cho nhé ! Thank you !
các bn ơi , bn nào biến đổi đưa về dạng những hằng đẳng thức cũng được nữa nhá !
Đúng 0
Bình luận (0)
Bài 3: Khi chia đa thức Pleft(xright)x^{81}+ã^{57}+bx^{41}+cx^{19}+2x+1 được số dư là 5 và khi chia đa thức P(x) cho (x-2) được số dư là -4
a) Hãy tìm các số thực A,B biết đa thức Qleft(xright)x^{81}+ã^{57}+bx^{41}+cx^{19}+Ax+B chia hết cho đa thức x^2-3x+2
b) Với giá trị của A và B vừa tìm được, hãy tính giá trị của đa thức
Rleft(xright)Qleft(xright)-Pleft(xright)+x^{81}+x^{57}-2x^{41}+2x^{19}+2x+1tại x 1,032016
Đọc tiếp
Bài 3: Khi chia đa thức \(P\left(x\right)=x^{81}+ã^{57}+bx^{41}+cx^{19}+2x+1\) được số dư là 5 và khi chia đa thức P(x) cho (x-2) được số dư là -4
a) Hãy tìm các số thực A,B biết đa thức \(Q\left(x\right)=x^{81}+ã^{57}+bx^{41}+cx^{19}+Ax+B\) chia hết cho đa thức \(x^2-3x+2\)
b) Với giá trị của A và B vừa tìm được, hãy tính giá trị của đa thức
\(R\left(x\right)=Q\left(x\right)-P\left(x\right)+x^{81}+x^{57}-2x^{41}+2x^{19}+2x+1\)tại x = 1,032016
Bài 3: Khi chia đa thức Px^{81}+ax^{57}+bx^{41}+cx^{19}+2x+1 được số dư là 5 và khi chia đa thức P(x) cho (x-2) được số dư là -4
a) Hãy tìm các số thực A,B biết đa thức Qleft(xright)x^{81}+ax^{57}+bx^{41}+cx^{19}+Ax+B chia hết cho đa thức x^2-3x+2
b) Với giá trị của A và B vừa tìm được, hãy tính giá trị của đa thức
Rleft(xright)Qleft(xright)-Pleft(xright)+x^{81}+x^{57}-2x^{41}+2x^{19}+2x+1tại x 1,032016
Đọc tiếp
Bài 3: Khi chia đa thức \(P=x^{81}+ax^{57}+bx^{41}+cx^{19}+2x+1\) được số dư là 5 và khi chia đa thức P(x) cho (x-2) được số dư là -4
a) Hãy tìm các số thực A,B biết đa thức \(Q\left(x\right)=x^{81}+ax^{57}+bx^{41}+cx^{19}+Ax+B\) chia hết cho đa thức \(x^2-3x+2\)
b) Với giá trị của A và B vừa tìm được, hãy tính giá trị của đa thức
\(R\left(x\right)=Q\left(x\right)-P\left(x\right)+x^{81}+x^{57}-2x^{41}+2x^{19}+2x+1\)tại x = 1,032016
Bài 1: Làm tính nhân
a. \(\left(2x^{2n}+3x^{2n-1}\right)\left(x^{1-2n}-3x^{2-2n}\right)\)
b. \(\left(25x^2+10xy+4y^2\right)\left(5x-2y\right)\)
c. \(\left(5x^3-x^2+2x-3\right)\left(4x^2-x+2\right)\)
a: \(=2x^{2n+1-2n}-2\cdot x^{2n}\cdot3\cdot x^{2-2n}+3\cdot x^{2n-1+1-2n}-9\cdot x^{2n-1+2-2n}\)
\(=2x-6x^2+3-9x\)
\(=-6x^2-7x+3\)
b: \(=\left(5x\right)^3-\left(2y\right)^3=125x^3-8y^3\)
Đúng 0
Bình luận (0)
Làm tính chia :
a) \(\left(6x^3-7x^2-x+2\right):\left(2x+1\right)\)
b) \(\left(x^4-x^3+x^2+3x\right):\left(x^2-2x+3\right)\)
c) \(\left(x^2-y^2+6x+9\right):\left(x+y+3\right)\)
a) \(\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right)\)

b) $(x^4-x^3+x^2+3x):(x^2-2x+3)$

c) \(\left( {{x^2} + {y^2} + 6x + 9} \right):\left( {x + y + 3} \right)\)
\(=\left( {{x^2} + 6x + 9 - {y^2}} \right)\left( {x + y + 3} \right)\)
\(=\left[ {\left( {{x^2} + 2x.3 + {3^2}} \right) - {y^2}} \right]:\left( {x + y + 3} \right)\)
\(=\left[ {{{\left( {x + 3} \right)}^2} - {y^2}} \right]:\left( {x + y + 3} \right)\)
\(=\left( {x + 3 - y} \right)\left( {x + 3 + y} \right):\left( {x + y + 3} \right)\)
$= x + 3 - y$
$= x - y + 3$
Đúng 0
Bình luận (0)
(6x3 - 7x2 - x + 2) : (2x + 1)
= (6x3 + 3x2 - 10x2 - 5x + 4x + 2) : (2x + 1)
= [(6x3 + 3x2) - (10x2 + 5x) + (4x + 2)] : (2x + 1)
= [3x2(2x + 1) - 5x(2x + 1) + 2(2x + 1)] : (2x + 1)
= (3x2 - 5x + 2)(2x + 1) : (2x + 1)
= 3x2 - 5x + 2
(x4 - x3 + x2 + 3x) : (x2 - 2x + 3)
= (x4 + x3 - 2x3 - 2x2 + 3x2 + 3x) : (x2 - 2x + 3)
= [(x4 + x3) - (2x3 + 2x2) + (3x2 + 3x)] : (x2 - 2x + 3)
= [x3(x + 1) - 2x2(x + 1) + 3x(x + 1)] : (x2 - 2x + 3)
= (x3 - 2x2 + 3x)(x + 1) : (x2 - 2x + 3)
= x(x2 - 2x + 3)(x + 1): (x2 - 2x + 3)
= x(x + 1)
= x2 + x
(x2 - y2 + 6x + 9) : (x + y + 3)
= [(x2 + 6x + 9) - y2] : (x + y + 3)
= [(x + 3)2 - y2] : (x + y + 3)
= (x + 3 + y)(x + 3 - y) : (x + y + 3)
= (x + y + 3)(x - y + 3) : (x + y + 3)
= x - y + 3
CHÚC BN HOK TỐT ![]()
![]()
![]()
Đúng 0
Bình luận (0)
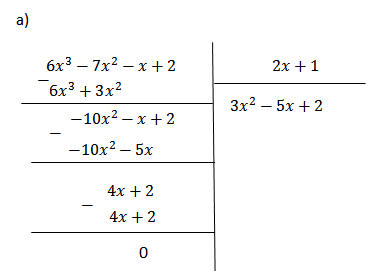
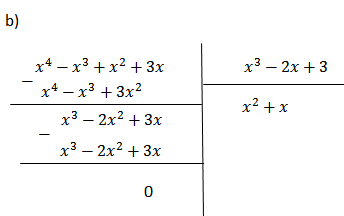
c) (x2+y2+6x+9):(x+y+3)
= (x2+6x+9−y2)(x+y+3)
= [(x2+2x.3+32)−y2]:(x+y+3)
= [(x+3)2−y2]:(x+y+3)
= (x+3−y)(x+3+y):(x+y+3)
= x + 3 - y
= x - y + 3
Đúng 0
Bình luận (2)
Xem thêm câu trả lời
Bài 1 : Ko thực hiện phép chia , hãy xem phép chia sau đây có là phép chia hết ko và tìm đa thức dư trong trg hợp ko chia hết :
a) \(\left(x^3+2x^2-3x+9\right):\left(x+3\right)\)
b) \(\left(9x^4-6x^3+15x^2+2x+1\right):\left(3x^2-2x+5\right)\)
b)\(\frac{9x^4-6x^3+15x^2+2x+1}{3x^2-2x+5}=\frac{3x^2.\left(3x^2-2x+5\right)+2x+1}{3x^2-2x+5}=3x^2+\frac{2x+1}{3x^2-2x+5}\)
=> đa thức dư trong phép chia là 2x+1
\(\frac{x^3+2x^2-3x+9}{x+3}=\frac{x^3+9x^2+27x+27-7x^2-30x-18}{x+3}=\frac{\left(x+3\right)^3-7x^2-30x-18}{x+3}\)
\(\left(x+3\right)^2-\frac{7x^2+21x+9x+18}{x+3}=\left(x+3\right)^2-\frac{7x.\left(x+3\right)+9.\left(x+3\right)-9}{x+3}\)
\(=\left(x+3\right)^2-\frac{\left(7x+9\right).\left(x+3\right)-9}{x+3}=\left(x+3\right)^2-\left(7x+9\right)-\frac{9}{x+3}\)
=> đa thức dư trong phép chia là 9
p/s: t mới lớp 7_sai sót mong bỏ qua :>
Đúng 0
Bình luận (0)
LÀM TÍNH CHIA:
a) \(\left(6x^6+2x^5-2x^4-15x^3+x^2+7x+2\right):\left(3x^2+x-1\right)\)
b) \(\left(-6x^4+5x^3+17x^2-23x+7\right):\left(-3x^2-2x+7\right)\)
Giải các phương trình sau:
a) x^2+dfrac{2x}{x-1}8
b) dfrac{x^2+2x+1}{x^2+2x+2}+dfrac{x^2+2x+2}{x^2+2x+3}dfrac{7}{6}
c) dfrac{x+4}{x-1}+dfrac{x-4}{x+1}dfrac{x+8}{x-2}+dfrac{x-8}{x+2}+6
d) left(x^2+6x+8right)left(x^2+8x+15right)24
e) left(x^2+x-2right)left(x^2+9x+18right)28
f) 3left(-x^2+2x+3right)^4-26x^2left(-x^2+2x+3right)^2-9x^40
g) x^4+6x^3+11x^2+6x+10
h) left(x-3right)left(x-5right)left(x-6right)left(x-10right)-24x^20
i) left(x+2right)^4+left(x+8right)^4272
Đọc tiếp
Giải các phương trình sau:
a) \(x^2+\dfrac{2x}{x-1}=8\)
b) \(\dfrac{x^2+2x+1}{x^2+2x+2}+\dfrac{x^2+2x+2}{x^2+2x+3}=\dfrac{7}{6}\)
c) \(\dfrac{x+4}{x-1}+\dfrac{x-4}{x+1}=\dfrac{x+8}{x-2}+\dfrac{x-8}{x+2}+6\)
d) \(\left(x^2+6x+8\right)\left(x^2+8x+15\right)=24\)
e) \(\left(x^2+x-2\right)\left(x^2+9x+18\right)=28\)
f) \(3\left(-x^2+2x+3\right)^4-26x^2\left(-x^2+2x+3\right)^2-9x^4=0\)
g) \(x^4+6x^3+11x^2+6x+1=0\)
h) \(\left(x-3\right)\left(x-5\right)\left(x-6\right)\left(x-10\right)-24x^2=0\)
i) \(\left(x+2\right)^4+\left(x+8\right)^4=272\)
giải hết đống này chắc @@ quá,để tối đi,giờ t đi làm mấy bài ngắn ngắn
Đúng 0
Bình luận (1)
a) x2+\(\dfrac{2x}{x-1}\)=8(ĐKXĐ : x ≠ 1
⇔ x2(x-1)+2x =8⇔ x3 - x2 +2x - 8=0
⇔x3 - 23 -x2+2x =0⇔ (x-2)(x2 +x+1) -x(x-2)
⇔(x-2)(x2 +1)⇒x =2
x2 +1 =0⇒x2 -1⇒x ∈∅(loại)
vậy x =2
Đúng 0
Bình luận (2)
Giải phương trình :
a) \(x^2+\dfrac{2x}{x-1}=8\)
ĐKXĐ : \(x-1\ne0\Rightarrow x\ne1\)
Ta có : \(x^2+\dfrac{2x}{x-1}=8\)
\(\Leftrightarrow\) \(\dfrac{x^2\left(x-1\right)}{x-1}+\dfrac{2x}{x-1}=\dfrac{8\left(x-1\right)}{x-1}\)
\(\Rightarrow x^2\left(x-1\right)+2x=8\left(x-1\right)\)
\(\Leftrightarrow x^3-x^2+2x=8x-8\)
\(\Leftrightarrow x^3-x^2+2x-8x=-8\)
\(\Leftrightarrow x^3-x^2-6x+8=0\)
\(\Leftrightarrow\left(x^3-x^2\right)-\left(6x-8\right)=0\)
\(\Leftrightarrow x^2\left(x-1\right)-2\left(3x-4\right)=0\)
\(\Leftrightarrow\left(x^2-2\right)\left(x-1\right)\left(3x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2=0\\x-1=0\\3x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=1\\x=\dfrac{4}{3}\end{matrix}\right.\)
Đối chiếu với ĐKXĐ ta được \(x\in\left\{\sqrt{2};\dfrac{4}{3}\right\}\) thỏa mãn.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
























