hãy phát biểu định lí diễn tả bởi đầu bài
a//b cvong goc voi a
viết giả thiết kết luận của định lí
Hãy phát biểu các định lí được diễn tả bằng các hình 42, rồi viết giả thiết kết luận của từng định lí (xem Bài 5).
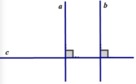
Nếu hai đường thằng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.

Hoặc: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó sẽ vuông góc với đường thẳng còn lại .
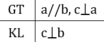
Hãy phát biểu các định lí được diễn tả bằng các hình 42, rồi viết giả thiết kết luận của từng định lí (xem Bài 5).
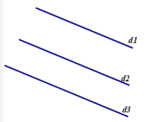
Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
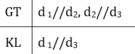
Hãy phát biểu định lí được diễn tả bằng giả thiết và kết luận sau (Hình 1):
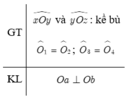
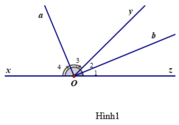
Định lí: Góc tạo bởi hai tia phân giác của hai góc kề bù là góc vuông
Hãy phát biểu các định lí được diễn tả bằng các hình vẽ sau, rồi viết giả thiết, kết luận của từng định lí (xem bài 5)
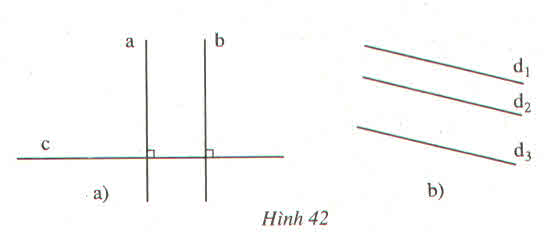
a) Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì đường thẳng đó song song với nhau.
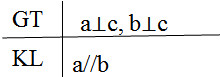
b) Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
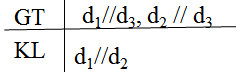
hình a) GT a phân biệt b
a vuông góc c
b vuông góc c
KL a // b
hình b) GT d1 // d3
d2 // d3
KL d1//d2
Cho các mệnh đề
P: “a và b chia hết cho c”;
Q: “a + b chia hết cho c”.
a) Hãy phát biểu định lí \(P \Rightarrow Q\). Nêu giả thiết, kết luận của định lí và phát biểu định lí này dưới dạng điều kiện cần, điều kiện đủ.
b) Hãy phát biểu mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) rồi xác định tính đúng sai của mệnh đề đảo này.
a) Mệnh đề \(P \Rightarrow Q\), phát biểu là: “Nếu a và b chia hết cho c thì a + b chia hết cho c.”
Mệnh đề này đúng nên nó là một định lý.
Giả thiết của định lí: a và b chia hết cho c
Kết luận của định lí: a + b chia hết cho c
Phát biểu định lí dưới dạng điều kiện cần là: “ a + b chia hết cho c là điều kiện cần để có a và b chia hết cho c”
Phát biểu định lí dưới dạng điều kiện đủ là: “ a và b chia hết cho c là điều kiện đủ để có a + b chia hết cho c”
b) Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề \(Q \Rightarrow P\).
Mệnh đề \(Q \Rightarrow P\): “Nếu a + b chia hết cho c thì a và b chia hết cho c”
Mệnh đề này sai.
Chẳng hạn a = 1 và b = 2, c =3. Ta có: \(1 + 2 = 3\; \vdots \;3\), nhưng 1 và 2 không chia hết cho 3.
1. Phát biểu, vẽ hình, ghi giả thiết - kết luận của định lí Ta-let, định lí đảo, hệ quả
2. Phát biểu, vẽ hình, ghi giả thiết - kết luận của tính chất đường phân giác trong tam giác
cho định lí : Góc tạo bởi hai tia phân giác của 2 góc kề bù là 1 góc vuông
- Hãy cho biết giả thiết của định lí
- Hãy cho biết kết luận của định lí
- Hãy chứng minh định lí trên
b, cho định lí :nếu 1 đường thẳng cắ 2 đường thẳng phân biệt và trong số các góc tạo thành có 1 cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau
- Hãy cho biết giả thiết của định lí đó
- Hãy cho biết kết luận của định lí đó
- Hãy chứng minh định lí đó
Nhanh là 1 Like nha !!!!!!!!!!!!!!!!!!
khó thì 10 like cũng ko được nữa là 1 like
a)
giả thiết vs kết luận bạn tự ghi nha, có đó dễ.
c/m:
gọi x và y là số đo góc tạo bởi 2 tia phân giác của 2 góc kề bù.
ta có: 2x + 2y= 180 độ
suy ra x+y = 180/2=90 độ
Bài 1 :
Giả thiết : Góc tạo bởi hai tia phân giác của 2 góc kề bù
Kết luận : là 1 góc vuông
Chứng minh :
gọi x và y là số đo góc tạo bởi 2 tia phân giác của 2 góc kề bù.
ta có: 2x + 2y= 180 độ
suy ra x+y = \(\dfrac{180^o}{90^o}\)=90 độ
Bài 2:
Giả thiết: Nếu một đường thẳng cắt 2 đường thẳng phân biệt trogn số các góc tạo thành có một cặp góc so le trong bằng nhau
Kết luận: thì các cặp góc đồng vị bằng nhau.
Hướng dẫn nha:
Bạn vẽ hai đường thẳng phân biệt song song vs nhau
Vẽ một đường thẳng bất kì đi qua 2 đưuòng thẳng song song đó.
Khi đó sẽ tạo thành hai cặp góc so le trong và đồng vị bằng nhau.
2 : Phát biểu tính chất : " Hai tia phân giác của 2 góc kề bù tạo thành góc vuông " thành định lí dạng : Nếu.... thì
rồi vẽ hình và ghi Giả thiết , kết luận của định lí
Chứng minh định lí và phát biểu
Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
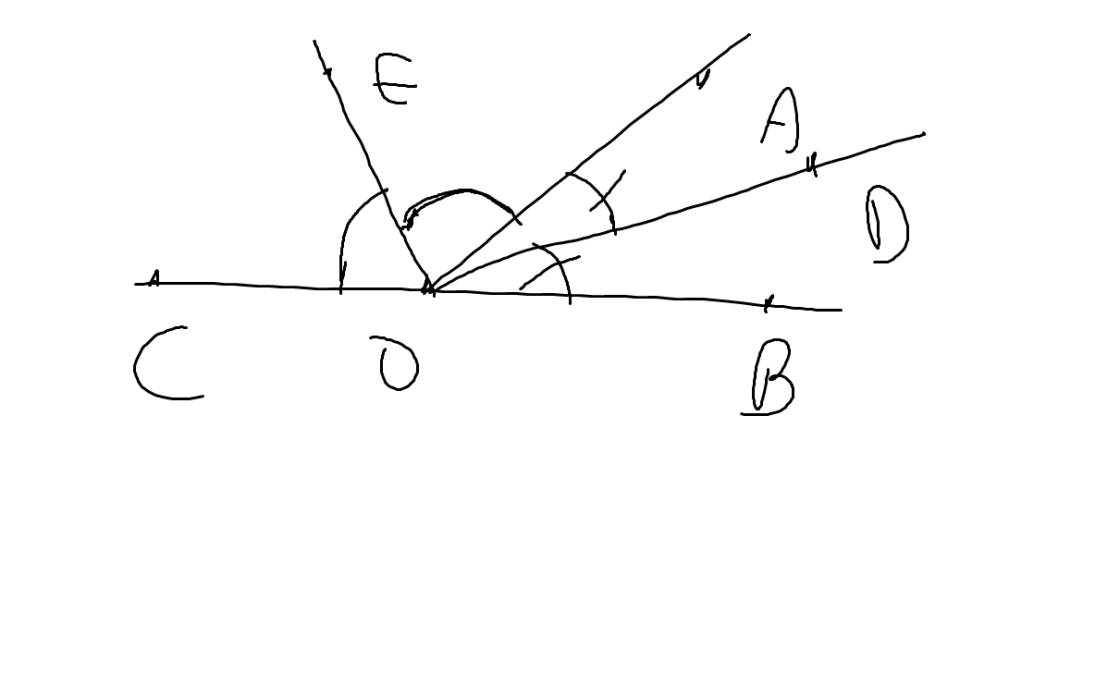
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)
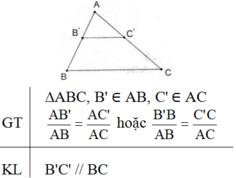
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet đảo.
Định lí Talet đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.