Cho (P): y=ax2 và A(1;1)
a) Tìm a để A(1;1) thuộc (P)
b) Gọi (D) là đường thẳng đi qua A và cắt trục Ox tại điểm M có hoành độ là m (m khác 1). Viết phương trình đường thẳng (D)
Cho (P): y = ax2+bx+1. Xác định a, b biết (P) qua M(1; 6) và trục đổi xứng x = -2
Theo đề, ta có:
-b/2a=-2 và a+b+1=6
=>b/2a=2 và a+b=5
=>2a=2b và a+b=5
=>a=b=2,5
Cho (P) y = ax2 + bx +3. Tìm a, b biết (P) đi qua A (-1; 6) và có tung độ đỉnh là 2
Cho (P):y=ax2 A)tìm a để (p) đi qua A(1;-2)vẽ (p) với a tìm được b)Cho(d):y=4x+1.tìm a để(p) và (d) có ít nhất một điểm chung
a: Thay x=1 và y=-2 vào (P), ta được:
a*1^2=-2
=>a=-2
=>y=-2x^2
b: PTHĐGĐ là:
ax^2-4x-1=0
Δ=(-4)^2-4*a*(-1)=4a+16
Để (P) và (d) có ít nhất 1 điểm chung thì 4a+16>=0
=>a>=-4
Cho hàm số y = x 3 + a x 2 + bx+1
Tìm a và b để đồ thị của hàm số đi qua hai điểm: A(1;2)và B(-2;-1)
Đồ thị hàm số đi qua A(1; 2) và B(-2; -1)
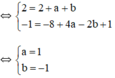
Cho parabol (P): y = a x 2 (a ≠ 0) đi qua điểm A (−2; 4) và tiếp xúc với đồ thị (d) của hàm số y = 2 (m – 1)x – (m – 1). Tọa độ tiếp điểm là:
A. (0; 0)
B. (1; 1)
C. A và B đúng
D. Đáp án khác
(P) đi qua điểm A (−2; 4) nên 4 = a. ( − 2 ) 2 = 4a a = 1
Vậy phương trình parabol (P) là y = x 2 .
Để (P) tiếp xúc với (d) thì phương trình hoành độ giao điểm
x 2 = 2 (m – 1)x – (m – 1)có nghiệm kép
↔ ∆ ’ = [ − ( m – 1 ) ] 2 − m + 1 = 0 ↔ m 2 – 2m + 1 − m + 1 = 0 ↔ m 2 – 3m + 2 = 0 ↔ m=1 hoặc m=2
Nếu m = 1 thì hoành độ giao điểm là x = 0. Vậy tiếp điểm là (0; 0)
Nếu m = 2 thì hoành độ giao điểm là x = 1. Vậy tiếp điểm là (1; 1)
Đáp án: C
Cho số thực a và hàm số y = a x 2 + 2018 x + 2019 - a x 2 + 2017 x + 2018 . Số tiệm cận nhiều nhất ( nếu có ) của đồ thị hàm số trên là
A. 3
B. 1
C. 2
D. 0
Đường thẳng d: y = mx + n và parabol (P): y = a x 2 ( a ≠ 0 ) tiếp xúc với nhau khi phương trình a x 2 = m x + n có:
A. Hai nghiệm phân biệt
B. Nghiệm kép
C. Vô nghiệm
D. Có hai nghiệm âm
Đáp án B
Đường thẳng d và parabol (P) tiếp xúc với nhau khi phương trình a x 2 = m x + n ⇔ a x 2 - m x - n = 0 có nghiệm kép ( Δ = 0 )
Câu 1: Cho đường thẳng (d1): y= (m-1)x+m-2 và đường thẳng (d2): y= -2x+3. Tìm giá trị của m để hai đường thẳng (d1) và (d2) song song với nhau
Câu 2: Cho (P): y= ax2 và hai điểm A (2;3), B(-1,0)
a) Tìm a biết rằng (p) đi qua M(1,2). Vẽ (P) với a vời tìm được
b) Tìm phương trình đường thẳng AB và tìm giao điểm của AB với (P)
(mink đag cần gấp)
Câu 1 :
Để (d1) // (d2) :
m - 1 = -2
=> m = -1
Câu 1: Cho đường thẳng (d1): y= (m-1)x+m-2 và đường thẳng (d2): y= -2x+3. Tìm giá trị của m để hai đường thẳng (d1) và (d2) song song với nhau
Câu 2: Cho (P): y= ax2 và hai điểm A (2;3), B(-1,0)
a) Tìm a biết rằng (p) đi qua M(1,2). Vẽ (P) với a vời tìm được
b) Tìm phương trình đường thẳng AB và tìm giao điểm của AB với (P)
(mink đag cần gấp)
1. Vì \((d_1)\parallel (d_2)\) \(\Rightarrow\left\{{}\begin{matrix}m-1=-2\\m-2\ne3\end{matrix}\right.\Rightarrow m=-1\)
2.a) (P) đi qua \(M\left(1;2\right)\Rightarrow2=a\Rightarrow y=2x^2\)
bạn tự vẽ nha
b) Gọi pt đường thẳng AB là \(y=ax+b\)
\(\Rightarrow\left\{{}\begin{matrix}3=2a+b\\0=-a+b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3=2a+b\left(1\right)\\0=-2a+2b\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)+\left(2\right)\Rightarrow3b=3\Rightarrow b=1\Rightarrow a=1\Rightarrow y=x+1\)
pt hoành độ giao điểm \(2x^2-x-1=0\Rightarrow\left(x-1\right)\left(2x+1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=2\\y=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\) tọa độ của 2 giao điểm là \(\left(1,2\right)\) và\(\left(-\dfrac{1}{2},\dfrac{1}{2}\right)\)
Xác định (P): y = ax2 + 2x + c biết (P) qua A (1; 0) và đỉnh I(3; -4)
Theo đề, ta có:
-2/2a=3 và -(2^2-4ac)/(4a)=-4 và a+2+c=0
=>a=-1/3 và c=-a-2=1/3-2=-5/3 và (4-4ac)/4a=4
=>Ko có (P) thỏa mãn