Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a. Bất phương trình \(ax + b < 0\) với \(a > 0\) có nghiệm là \(x < \frac{{ - b}}{a}\).
b. Bất phương trình \(ax + b < 0\) với \(a \ne 0\) có nghiệm là \(x < \frac{{ - b}}{a}\).
c. Bất phương trình \(ax + b < 0\) với \(a < 0\) có nghiệm là \(x > \frac{{ - b}}{a}\).
d. Bất phương trình \(ax + b < 0\) với \(a \ne 0\) có nghiệm là \(x > \frac{{ - b}}{a}\).











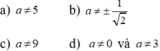
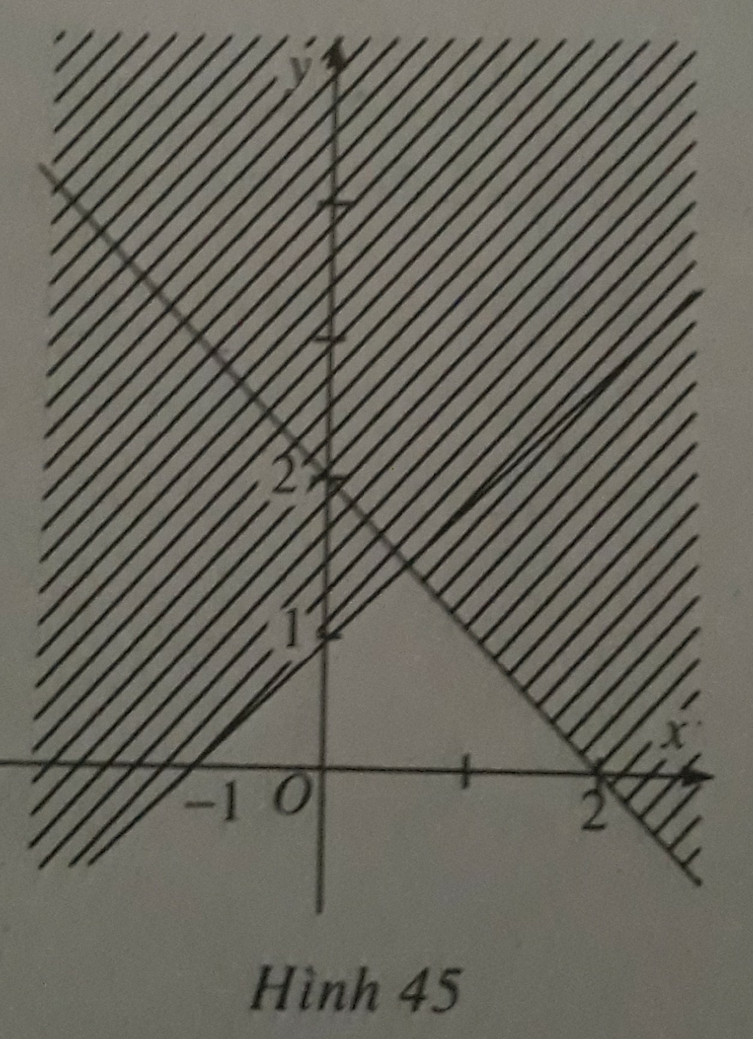
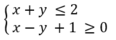 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.
