Cho d1: 2x-3y+5=0, d2: 3x+y+2=0. A là giao điểm của d1 và d2 có toạ độ A(-1;1).
Tìm toạ độ điểm B và C biết Bϵd1 và Cϵd2 sao cho O(0;0) là trọng tâm của △ABC

Những câu hỏi liên quan
Cho hàm số y=4-2x (d1) và y=3x+1 (d2) a) Vẽ (d1) và (d2) trên cùng mặt phẳng toạ độ b) Gọi A là giao điểm của (d1) và (d2). Tìm toạ độ giao điểm A c) Tính góc tạo bởi (d1) với trục hoành Tính góc tạo bởi (d2) với trục hoành
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}4-2x=3x+1\\y=3x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=\dfrac{9}{5}+1=\dfrac{14}{5}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số y = 2x có đồ thị là (D1) và hàm số y = 2 /1 x – 3 có đồ thị là (D2). a) Vẽ (D1), (D2) trên cùng một mặt phẳng toạ độ. b) Tìm toạ độ giao điểm của (D1) và (D2) bằng phép tính
Bạn ghi rõ đề ở chỗ (d2) là pt nào đi bạn
Đúng 0
Bình luận (0)
Cho hai đường thẳng: (d1):y=1/2x+2 và (d2):y=-x+2
a) vẽ (d1) và (d2) trên cùng một hệ trục toạ độ Oxy
b) gọi A là giao điểm của (d1) với trục hoành. Tìm toạ độ điểm A
c) gọi B là giao điểm của (d2) với trục tung. Tìm toạ đồ điểm B
d)gọi C là giao điểm của (d1) và (d2). Tìm toạ độ điểm C
Mông các bạn giải giúp mình gấp với ạ :3
a/ bạn tự làm
b/ \(\Rightarrow y=0\Rightarrow\dfrac{1}{2}x+2=0\) giải PT tìm hoành độ x
c/ \(\Rightarrow x=0\Rightarrow y=0+2=2\)
d/ \(\Rightarrow\dfrac{1}{2}x+2=-x+2\) Giải PT tìm hoành độ x của C rồi thay vào d1 hoặc d2 để tìm tung độ y của C
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy,cho hai đường thẳng d1:2x-y+5=0,d2:3x+6y-1=0 và điểm P(-2,0).Gọi A là giao điểm của d1 và d2.Khi đó đường thẳng d đi qua P và cùng với d1,d2 tạo thành một tam giác cân đỉnh A có phương trình là?
Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn
Đúng 1
Bình luận (0)
Câu 4: a, Vẽ y = 2/3x + 2 (d1) y = 2x+2 trên cùng mặt phẳng tọa độ b, Gọi A,B là giao điểm d1 và d2 với trục Ox và giao d1 với d2 là C : Tìm toạ độ giao điểm A,B,C
a:
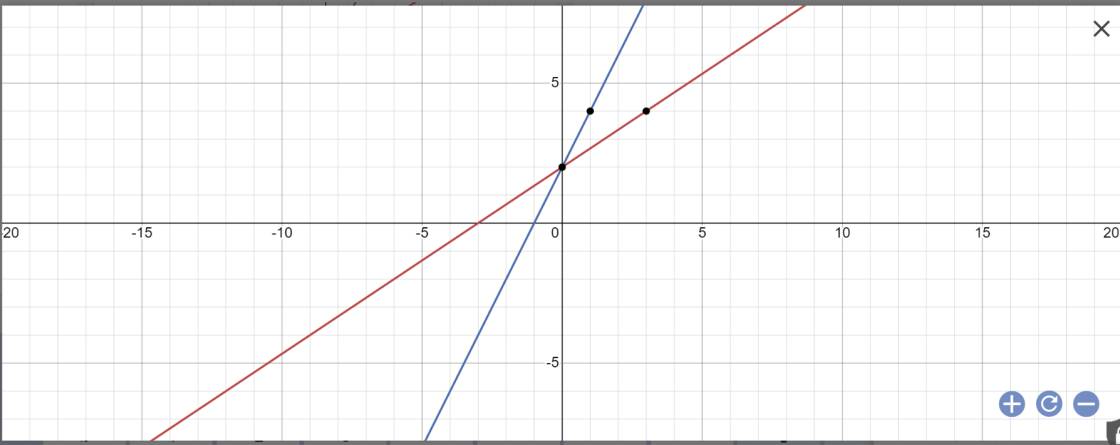
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{2}{3}x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\dfrac{2}{3}x=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=-2:\dfrac{2}{3}=-2\cdot\dfrac{3}{2}=-3\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\2x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}\dfrac{2}{3}x+2=2x+2\\y=2x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{4}{3}x=0\\y=2x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=2\cdot0+2=2\end{matrix}\right.\)
Vậy: A(-3;0); B(-1;0); C(0;2)
Đúng 2
Bình luận (0)
Cho hàm số y=3x(d1);y=-2x-5(d2).
a)Vẽ (d1);(d2) trên cùng một mặt phẳng toạ độ. Tìm toạ độ A là giao của chúng.
b)Viết phương tình đường thẳng (d3) đi qua A và cắt trục tung tại điểm có tung độ là -2.
c)Tìm m để điểm C(3;m) thuộc (d3).
Xem chi tiết
Cho y x 3 d1 , y 3x 1 d2 . a vẽ d1,d2 trên cùng 1 mặt phẳng toạ độ .b tìm toạ độ giao điểm của d1 và d2. Giúp em nhanh em đang cần gấp ạ
Bạn ghi lại đề đi bạn. Khó hiểu quá!
Đúng 0
Bình luận (0)
Cho y x 3 d1 , y 3x 1 d2 . a vẽ d1,d2 trên cùng 1 mặt phẳng toạ độ .b tìm toạ độ giao điểm của d1 và d2. Giúp em nhanh em đang cần gấp ạ
Bạn ghi lại đề đi bạn, khó hiểu quá!
Đúng 0
Bình luận (0)
cho ba đường thẳng d1:y=3x,d2:y=1/3x,d3:y=-x+4 a,vẽ d1,d2,d3 trên cùng mặt phẳng toạ độ b,gọia,b lần lượt là giao điểm của d1 và d2.tìm toạ độ của a và b c,chứng minh tam giác OAB cân d,tính diện tích tam giác OAB
a: 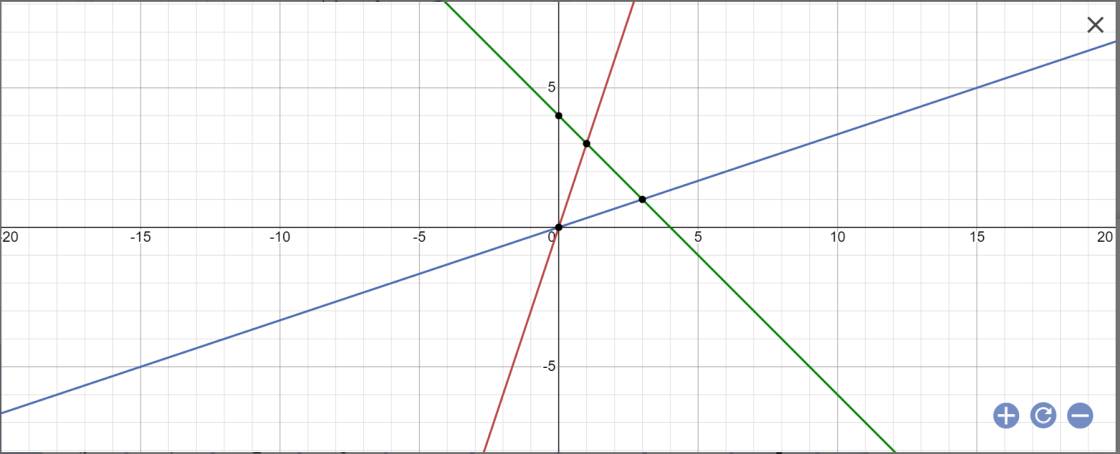
b:
Bổ sung đề: A,B lần lượt là giao của (d1) với (d2) và (d3)
Tọa độ A là:
3x=1/3x và y=3x
=>x=0 và y=0
Tọa độ B là:
3x=-x+4 và y=3x
=>x=1 và y=3
Đúng 0
Bình luận (0)
Cho hàm số y=2x (D1) và y=-1/2 x+3(D2)
a. vẽ D1 và D2 lên cùng hệ trục
b. tìm toạ độ giao điểm D1 và D2 bằng đồ thị và phép toán
c. Tìm điểm thuộc D1 có tung độ kém 2 lần hoành độ
mình cần gấp á ai giúp mình với
Đúng 0
Bình luận (0)
b. \(PTHDGD:\left(D1\right)-\left(D2\right):2x=-\dfrac{1}{2}x+3\)
\(=>x=\dfrac{6}{5}\)
Thay x = \(\dfrac{6}{5}\) vào (D1): \(y=2\cdot\dfrac{6}{5}=\dfrac{12}{5}\)
Vậy (D1) cắt (D2) tại \(A\left(\dfrac{6}{5};\dfrac{12}{5}\right)\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời