Cho a-b = -5
Tính giá trị biểu thức :P=(a-b)^3-a^2+2ab-b^2
Những câu hỏi liên quan
cho a>b>0 và a^2-6b^2=ab. Tính giá trị biểu thức : A=(2ab)/(a^2-7b^2). Tính giá trị biểu thức : A=(2ab)/(a^2-7b^2)
Cho biết a - b =7.Tính giá trị biểu thức:
a(a+2)+b(b-2)-2ab
a(a + 2) + b(b - 2) - 2ab
= a2 + 2a + b2 - 2b - 2ab
= (a2 - 2ab + b2) +(2a - 2b)
= (a - b)2 + 2(a - b)
= 72 + 2.7
= 49 + 14 =63
Đúng 0
Bình luận (0)
\(a\left(a+2\right)+b\left(b-2\right)-2ab=a^2+2a+b^2-2b-2ab\)
\(=\left(a^2-2ab+b^2\right)+\left(2a-2b\right)=\left(a-b\right)^2+2\left(a-b\right)\)
Với \(a-b=7\)thì biểu thức có giá trị là: \(7^2-7=49-7=42\)
Nhầm dòng cuối \(7^2+7=49+7=56\)
Xem thêm câu trả lời
cho biết a-b=7 tính giá trị của biểu thức a(a+b) + b ( b-2 ) - 2ab
Bài 18 Tính giá trị của biểu thức :
a, x^2 + x-8 với x= -2
b, -5.x^3. | x-1 | +15 với x= -2
Bài 12 Cho a= -5 , b= -6 . Tính giá trị của biểu thức :
a, a^2 - 2ab + b^2 và (a-b)^2 ;
b, (a+b) . (a-b) và a^2 -b^2 ;
c, a^2 + 2ab b^2 và (a+b)^2
Từ kết quả nhận được , hãy nêu nhận xét
Tính giá trị biểu thức
( 2ab^2 ) : c với a = 4 ; b = -6 ; c= 12
( a^2 -2ab + b^2 ) : ( a+ b)( a+ b) với a= -7 ; b=4
( a^2 - b^2) : (a+b)(a-b) với a=5 ; b= -3
Tính giá trị của các biểu thức sau với |a| = 1,5; b = -0,75
M = a + 2ab – b
N = a : 2 – 2 : b
P = (-2) : a2 - b.(2/3)
Vì |a| = 1,5 nên a = 1,5 hoặc a = -1,5
Với a = 1,5; b = -0,75. Ta có:
M = 1,5 + 2.1,5( - 0,75) – (-0,75)
= 1,5 + ( -2,25) + 0,75
= (1,5 + 0,75) + (-2,25)
= 2,25 + (-2,25) = 0
N = 1,5 : 2 -2 : ( -0,75)
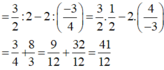
P = (-2) : (1,5)2 - (-0,75).(2/3)
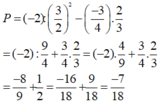
Với a = -1,5; b = -0,75 ta có:
M = - 1,5 + 2.(-1,5) ( - 0,75) – (-0,75)
= - 1,5 + ( 2,25) + 0,75
= (2,25+ 0,75) - 1,5
= 3 – 1,5 = 1,5
N = - 1,5 : 2 - 2 : ( -0,75)
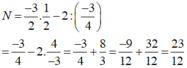
P = (-2) : (-1,5)2 — (-0,75).(2/3)
Đúng 0
Bình luận (0)
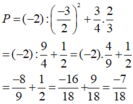
Tính các giá trị của biểu thức sau với |a|= 1,5 ; b= -0,75
M= a + 2ab - b
N=a : 2 - 2 :b
P= (-2) : a2 - b. 2/3
Chú ý: Tính mỗi biểu thức có hai giá trị
l al = 1,5 => a = 1,5 hoặc a = -1,5
(+) a = 1,5
M = 1,5 + 2.1,5.-0,75 - - 0,75 = 1,5 + 3.-0,75 + 0,75 = 0
N , P tính tương tự
(+) a = -1,5 ; b = -0,75 thay vào ta có
M = ....
Tự làm tiếp nha
Đúng 0
Bình luận (0)
Cho biết a+b=1 , tính giá trị biểu thức A=a^2+2ab+b^2+4a+4b+2015
Giúp mình với mng
\(a^2+2ab+b^2+4a+4b+2015\\ =\left(a+b\right)^2+4\left(a+b\right)+2015\\ =\left(a+b\right)\left(a+b+4\right)+2015\\ =1.\left(1+4\right)+2015\\ =5+2015\\ =2020\)
Đúng 1
Bình luận (0)
\(A=\left(a+b\right)^2+4\left(a+b\right)+2015=2020\)
Đúng 0
Bình luận (0)
4 tháng 12 2023 lúc 17:16
Cho hai số thực không âm \(a\) và \(b\), biết \(a^2+b^2=6\). Tìm giá trị lớn nhất của biểu thức \(P=\dfrac{2ab}{a+b+2}\)