-         Số phần tử của không gian mẫu là: \(n\left( \Omega  \right) = 3! = 6\)

-         Gọi B là biến cố “Không lá thư nào được bỏ đúng phong bì”

A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”

⇨     n(B) = 2

⇨     \(P(A) = 1 - P(B) = 1 - \frac{2}{6} = \frac{2}{3}\)

Đáp án A

Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất

Lời giải:

Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.

Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.

Gọi U là tập hợp các cách bỏ thư và A_m là tính chất lá thư thứ m bỏ đúng địa chỉ.

Khi đó, theo công thức về nguyên lý bù trừ, ta có  N ¯ = 4 ! - N 1 + N 2 - . . . + ( - 1 ) 4 N 4 .

Trong đó N_m ( 1 ≤ m ≤ 4 ) là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.

Nhận xét rằng, N_m là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có (4 - m)! cách bỏ m lá thư này đúng địa chỉ, ta nhận được:

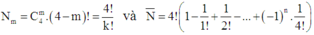
Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là

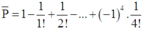
Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là  P = 1 - P ¯ = 5 8 .

Đáp án A

Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất

Lời giải:

Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.

Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.

Gọi U là tập hợp các cách bò thư và A m  là tính chất lá thư thứ m bỏ đúng địa chỉ.

Khi đó, theo công thức về nguyên lý bù trừ, ta có N ¯ = 4 ! − N 1 + N 2 − ... + − 1 4 N 4  

Trong đó N m 1 ≤ m ≤ 4  là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.

Nhận xét rằng, N m  là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có 4 − m !  cách bỏ m lá thư này đúng địa chỉ, ta nhận được: N m = C 4 m . 4 − m ! = 4 ! k !  và 

N ¯ = 4 ! 1 − 1 1 ! + 1 2 ! − ... + − 1 n . 1 4 !

Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là  P ¯ = 1 − 1 1 ! + 1 2 ! − ... + − 1 4 . 1 4 !

Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là  P = 1 − P ¯ = 5 8

Người gửi / From : Nguyễn Bảo Nam
Số 9, ngõ 233, Đường Xuân Thủy, Cầu Giấy, Hà Nội
Người nhận / To : Phan Hoàng Hải.

Tà Xùa, Bắc Yên, Sơn La.

1 em mỗi giờ làm được:

400 : (4 x 25)= 4(phong bì)

45 em 1 giờ làm được:

4 x 45= 180(phong bì)

45 em làm 940 phong bì trong:

940:180= 47/9(giờ)

Bài của anh pop pop làm là rất chính xác tuy nhiên kết  quả cuối cùng cần đổi ra 

              Đổi \(\dfrac{47}{9}\) giờ = 5 giờ 13 phút 20 giây 

            Đáp số: 5 giờ 13 phút 20 giây

            Đối với những bài toán về thời gian thì phải đổi ra nếu có thể nếu không sẽ  bị trừ 0,25 điểm

Đáp án D

Số phần tử không gian mẫu là:  n ( Ω ) = 3 ! = 6 .

Gọi A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”.

Ta xét các trường hợp sau:

Nếu lá thứ nhất bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.  

Nếu lá thứ hai bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.

Nếu lá thứ ba bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.

Không thể có trường hợp hai lá thư bỏ đúng và một lá thư bỏ sai.

Cả ba lá thư đều được bỏ đúng có duy nhất 1 cách.

⇒ n A = 4

Vậy xác suất để có ít nhất một lá thư được bỏ đúng phong bì là:

  P ( A ) = n ( A ) n Ω = 4 6 = 2 3 .

Cách 2:

Gọi B là biến cố “Không có lá thư nào được bỏ đúng phong bì”.

⇒ n B = 2

P ( A ) = 1 - P ( B ) = 1 - n ( B ) n Ω = 1 - 2 6 = 2 3 .

Chọn B

Xét các dãy số x 1 ; x 2 ; x 3 , trong đó x 1 ; x 2 ; x 3 là một hoán vị của ba số 1,2,3 (ở đây x i = i , tức là lá thư i đã bỏ đúng địa chỉ).

Gọi Ω là tập hợp tất cả các khả năng bỏ 3 lá thư vào 3 phong bì. Khi đó Ω = 3 ! = 6 .

Gọi A là biến cố: “Có ít nhât 1 lá thư bỏ đúng phong bì”. Các khả năng thuận lợi của A là ( 1;2;3 ); ( 1;3;2 ); ( 3;2;1 ); ( 2;1;3 ). Do vậy Ω A = 4 .

Từ đó P ( A ) = Ω A Ω = 4 6 = 2 3

Đáp án cần chọn là A