Tập viết phong bì thư.

Những câu hỏi liên quan
Tập ghi trên phong bì thư

b. Viết trên phong bì thư: họ và tên, địa chỉ của em và người bạn sẽ nhận thư.
Người gửi / From : Nguyễn Bảo Nam
Số 9, ngõ 233, Đường Xuân Thủy, Cầu Giấy, Hà Nội
Người nhận / To : Phan Hoàng Hải.
Tà Xùa, Bắc Yên, Sơn La.
Đúng 0
Bình luận (0)
Một người cho ngẫu nhiên 3 lá thư vào 3 chiếc phong bì đã ghi địa chỉ sao cho mỗi phong bì chỉ chứa một lá thư. Tính xác suất để có ít nhất một lá thư được cho vào đúng phong bì đã ghi địa chỉ theo lá thư đó.
- Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = 3! = 6\)
- Gọi B là biến cố “Không lá thư nào được bỏ đúng phong bì”
A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”
⇨ n(B) = 2
⇨ \(P(A) = 1 - P(B) = 1 - \frac{2}{6} = \frac{2}{3}\)
Đúng 0
Bình luận (0)
Một người bỏ ngẫu nhiên ba lá thư vào ba chiếc phong bì đã ghi địa chỉ. Xác suất để có ít nhất một lá thư được bỏ đúng phong bì là A.
1
3
B.
5
6
C.
1
2
D.
2
3
Đọc tiếp
Một người bỏ ngẫu nhiên ba lá thư vào ba chiếc phong bì đã ghi địa chỉ. Xác suất để có ít nhất một lá thư được bỏ đúng phong bì là
A. 1 3
B. 5 6
C. 1 2
D. 2 3
Đáp án D
Số phần tử không gian mẫu là: n ( Ω ) = 3 ! = 6 .
Gọi A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”.
Ta xét các trường hợp sau:
Nếu lá thứ nhất bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.
Nếu lá thứ hai bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.
Nếu lá thứ ba bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.
Không thể có trường hợp hai lá thư bỏ đúng và một lá thư bỏ sai.
Cả ba lá thư đều được bỏ đúng có duy nhất 1 cách.
⇒ n A = 4
Vậy xác suất để có ít nhất một lá thư được bỏ đúng phong bì là:
P ( A ) = n ( A ) n Ω = 4 6 = 2 3 .
Cách 2:
Gọi B là biến cố “Không có lá thư nào được bỏ đúng phong bì”.
⇒ n B = 2
P ( A ) = 1 - P ( B ) = 1 - n ( B ) n Ω = 1 - 2 6 = 2 3 .
Đúng 0
Bình luận (0)
Một người bỏ ngẫu nhiên ba lá thư vào ba chiếc phong bì đã ghi địa chỉ. Tính xác suất để ít nhất có một lá thư bỏ đúng phong bì của nó
A. 1 3
B. 2 3
C. 2 5
D. 1 2
Gía tiền một phong bì là 200 đồng , giá tiền một tem thư nhiều hơn giá tiền một phong bì là 600 đồng . Hỏi giá tiền một tem thư là bao nhiêu ?
giá tiền một tem thư là: 200+600=800 ( đồng)
Đúng 0
Bình luận (0)
Giá tiền một tem thư là:
200+600=800(đồng)
Đáp số:800 đồng.
Cho đúng nhé khampha
Đúng 0
Bình luận (0)
Giá tiền một tem thư là:
200 + 600 = 800 ( đồng )
Đáp số: 800 đồng.
cho mình đúng với nha các bạn thân mến !!!!!!!!!!!!!!!!!!!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
giá tiền một phong bì là 200 đồng , giá tiền một tem thư nhiều hơn giá tiền một phong bì là 600 đồng . Hỏi giá tiền một tem thư là bao nhiêu ?
gía tiền của một tem thư là:
200+600=800
mọi người biết bài giải là sao ko ?
Xem thêm câu trả lời
có 8 con tem và 5 phong bì thư.Chọn ra 3 con tem để dán vào 3 bì thư, mỗi bì thư dán 1 con tem.Hỏi có bao nhiêu cách dán?
Một người bỏ ngẫu nhiên 4 lá thư vào 4 bì thư đã được ghi sẵn địa chỉ cần gửi. Tính xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó. A.
5
8
. B.
1
8
.
C.
3
8
. D.
7
8
.
Đọc tiếp
Một người bỏ ngẫu nhiên 4 lá thư vào 4 bì thư đã được ghi sẵn địa chỉ cần gửi. Tính xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó.
A. 5 8 .
B. 1 8 .
C. 3 8 .
D. 7 8 .
Đáp án A
Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất
Lời giải:
Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.
Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.
Gọi U là tập hợp các cách bỏ thư và Am là tính chất lá thư thứ m bỏ đúng địa chỉ.
Khi đó, theo công thức về nguyên lý bù trừ, ta có N ¯ = 4 ! - N 1 + N 2 - . . . + ( - 1 ) 4 N 4 .
Trong đó Nm ( 1 ≤ m ≤ 4 ) là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.
Nhận xét rằng, Nm là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có (4 - m)! cách bỏ m lá thư này đúng địa chỉ, ta nhận được:
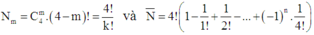
Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là
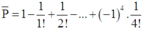
Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là P = 1 - P ¯ = 5 8 .
Đúng 0
Bình luận (0)
Một người bỏ ngẫu nhiên 4 lá thư vào 4 bì thư đã được ghi sẵn địa chỉ cần gửi. Tính xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó A.
5
8
B.
1
8
C.
3
8
D.
7
8
Đọc tiếp
Một người bỏ ngẫu nhiên 4 lá thư vào 4 bì thư đã được ghi sẵn địa chỉ cần gửi. Tính xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó
A. 5 8
B. 1 8
C. 3 8
D. 7 8
Đáp án A
Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất
Lời giải:
Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.
Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.
Gọi U là tập hợp các cách bò thư và A m là tính chất lá thư thứ m bỏ đúng địa chỉ.
Khi đó, theo công thức về nguyên lý bù trừ, ta có N ¯ = 4 ! − N 1 + N 2 − ... + − 1 4 N 4
Trong đó N m 1 ≤ m ≤ 4 là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.
Nhận xét rằng, N m là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có 4 − m ! cách bỏ m lá thư này đúng địa chỉ, ta nhận được: N m = C 4 m . 4 − m ! = 4 ! k ! và
N ¯ = 4 ! 1 − 1 1 ! + 1 2 ! − ... + − 1 n . 1 4 !
Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là P ¯ = 1 − 1 1 ! + 1 2 ! − ... + − 1 4 . 1 4 !
Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là P = 1 − P ¯ = 5 8
Đúng 0
Bình luận (0)

















