Cho tam giác ABC nhọn, M là điểm bất kỳ trên cạnh BC (M khác B;C). Từ M vẽ ME//AC với E thuộc AB, vẽ MF//AB với F thuộc AC. Chứng minh AE.EB + AF.FC > BM.MC

Những câu hỏi liên quan
Cho tam giác ABC với AB ≤ AC. Trên cạnh BC lấy một điểm M bất kỳ khác B và C. Chứng minh rằng AM < AC.
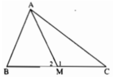
ΔABC có AB ≤ AC ⇒ ∠C ≤ ∠B.
ΔABM có ∠M1 là góc ngoài nên ∠M1 > ∠B
⇒ ∠M1 > ∠C
ΔAMC có ∠M1 > ∠C ⇒ AC > AM.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn (AB < AC). Gọi M là điểm bất kỳ trên BC. Vẽ N đối xứng của M qua AB.a) C/m:tam giác ABN = tam giác ABM b) Lấy D thuộc AB. C/m: tam giác AND = tam giác ADM
a: Ta có: M và N đối xứng nhau qua AB
nên AB là đường trung trực của MN
Suy ra: AM=AN; BM=BN
Xét ΔABN và ΔABM có
AB chung
BN=BM
AN=AM
Do đó: ΔABN=ΔABM
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A (BAC <90°), Kẻ BI vuông góc với AC tại 1. Trên cạnh BC lấy điểm M bất kỳ (M khác B và C). Gọi D, E, F lần lượt là chân đường vuông góc kẻ từ M đến các cạnh AB, AC, BI. 1) Chứng minh rằng tam giác DBM = tam giác FMB. 2) Cho BC = 10cm, CI = 6cm. Tính tổng MD + ME. 3) Trên tia đối của tia CA lấy điểm K sao cho CK = EI. Chứng minh BC đi qua trung điểm của đoạn thẳng DK.
Cho tam giác ABC, M là một điểm bất kỳ trên BC và M khác trung điểm BC. Hãy vẽ qua M một đường thẳng sao cho đường thẳng đó chia tam giác ABC thành hai phần có diện tích bằng nhau
Giả sử BM<MC khi đó: S(AMB)<S(AMC) Đặt I là trung điểm BC. Nối AM, AI. Qua I kẻ đường thẳng song song với AM và cắt AC tại N và AI giao với MN tại O. Đường thẳng MN chính là đường thẳng cần phải vẽ. Thật vây, tứ giác ANIM là hình thang nên S(AON)=S(MOI) Mặt khác: S(AIC)=1/2S(ABC)=S(AON)+S(CION)=S(MOI)+S(CION)=S(CMN)
Đúng 0
Bình luận (0)
Cho tam giác ABC, M là một điểm bất kỳ trên BC và M khác trung điểm BC. Hãy vẽ qua M một đường thẳng sao cho đường thẳng đó chia tam giác ABC thành hai phần có diện tích bằng nhau
Giả sử BM<MC khi đó: S(AMB)<S(AMC)
Đặt I là trung điểm BC. Nối AM, AI. Qua I kẻ đường thẳng song song với AM và cắt AC tại N và AI giao với MN tại O.
Đường thẳng MN chính là đường thẳng cần phải vẽ.
Thật vây, tứ giác ANIM là hình thang nên S(AON)=S(MOI)
Mặt khác:
S(AIC)=1/2S(ABC)=S(AON)+S(CION)=S(MOI)+S(CION)=S(CMN)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân ở A,B vuông góc AC tại H. Trên cạnh BC lấy điểm M bất kỳ(M khác B và C). Gọi D;E;F lần lượt là chân đường vuông góc kẻ từ M đến AB;AC và BH.
A) CM: tam giác DBM= tam giác FMB
b) Khi M chạy trên cạnh BC thì tổng MD+ ME không đổi
c) Trên tia đối của tia CA lấy K sao cho KC=EH. CM: BC đi qua trung điểm của DK
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Trên cạnh AB lấy điểm M sao cho AM = 2cm. Từ M kẻ đường thẳng song song với BC cắt AC tại N. a) Tính độ dài các đoạn thẳng MN, NC. b) Lấy điểm I bất kỳ trên cạnh BC (I khác B, C). Vẽ điểm O trên đoạn AI sao AI = 3AO. Chứng minh ba điểm M, N, O thẳng hàng.
cho tam giác ABC,góc B=90 độ,BA=BC. Gọi M là trung điểmcyả AC,D là điểm bất kỳ trên cạnh AC(D khác A,C,M). Kẻ AH,CK vuông góc với BD.CMR: AH song song CK và CK=BH
Bài 1: Cho tam giác ABC, gọi M,N lần lượt là trung điểm của AB, AC.a)Chứng minh MN // BCb)Gọi D là điểm bất kỳ thuộc cạnh BC ( D khác B,C), AD cắt MN tại I. Chứngminh I là trung điểm của AD.Bài 2: Cho tam giác ABC cân tại A, M là trung điểm của BC. Kẻ Mx// AC cắt AB tại E, kẻ My// AB cắt AC tại F. Chứng minh rằng:1)E,F là trung điểm của AB, AC2) FE 1/2 BC3) MEMF, AEFA
Đọc tiếp
Bài 1: Cho tam giác ABC, gọi M,N lần lượt là trung điểm của AB, AC.
a)Chứng minh MN // BC
b)Gọi D là điểm bất kỳ thuộc cạnh BC ( D khác B,C), AD cắt MN tại I. Chứng
minh I là trung điểm của AD.
Bài 2: Cho tam giác ABC cân tại A, M là trung điểm của BC. Kẻ Mx// AC cắt AB tại E, kẻ My// AB cắt AC tại F. Chứng minh rằng:
1)E,F là trung điểm của AB, AC
2) FE = 1/2 BC
3) ME=MF, AE=FA
Bài 1 : a) M là trung điểm AB
N là trung điểm AC
suy ra : MN là Đường trung bình của tam giác ABC
suy ra : MN // BC ; MN = BC/2
b) Ta có : MN // BC và M là trung điểm AB
Mà AD cắt MN tại I nên từ đó suy ra : I là trung điểm của cạnh AD
em chỉ giải được bài 1 thôi nên thông cảm ạ
Đúng 1
Bình luận (0)















