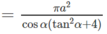hãy chỉ ra các đỉnh,cạnh bên,mặt bên,mặt đáy,đường cao,trung đoạn của hình chóp đều.
Cho hình chóp tứ giác đều \(A.MNPQ\) (Hình 5)
a) Hãy cho biết đỉnh, cạnh bên, mặt bên, cạnh đáy, mặt đáy, đường cao của hình chóp tứ giác đều đó.
b) Cho biết \(AM = 5\)cm, \(MN = 4\)cm. Tìm độ dài các cạnh \(AN\), \(AP\), \(AQ\), \(NP\), \(PQ\), \(QM\)

- Mặt bên: \(MAB\), \(MAC\), \(MBC\)
- Mặt đáy: \(ABC\)
- Đường cao: \(MO\)
- Độ dài cạnh bên: \(15\)cm
- Độ dài cạnh đáy: \(10\)cm
Quan sát hình chóp tam giác đều ở Hình 2 và cho biết:
a) Đỉnh, mặt đáy và các mặt bên của hình đó
b) Độ dài cạnh \(MA\) và cạnh \(BC\)
c) Đoạn thẳng nào là đường cao của hình đó.
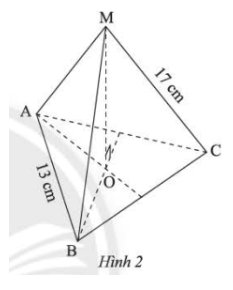
a) Đỉnh: \(M\)
Mặt đáy: \(ABC\)
Các mặt bên: \(MAB\); \(MAC\); \(MBC\)
b) Các cạnh bên bằng nhau: \(MA = MC = 17\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 13\)cm
c) Đoạn thẳng \(MO\) là đường cao của hình chóp tam giác đều \(M.ABC\)
Hãy cho biết mặt bên, mặt đáy, đường cao, độ dài cạnh bên, độ dài cạnh đáy của hình chóp tam giác đều ở Hình 3
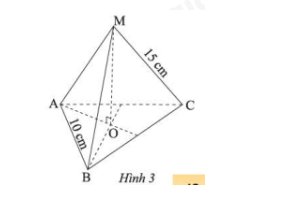
Các mặt bên là MAB, MAC, MBC
Các cạnh bên là MA = MB = MC = 15cm
Đường cao là MO
Các cạnh đáy là AB = AC = BC =10cm
Mặt bên: ΔAMB; ΔBMC; ΔAMC
Mặt đáy: ΔABC
Độ dài cạnh bên: 15cm
Độ dài cạnh đáy: 10cm
Cho hình chóp cụt tứ giác đều A B C D . A 1 B 1 C 1 D 1 có các cạnh đáy 5cm và 10cm, đường cao mặt bên bằng 5cm. Hãy tính: Tính cạnh bên và đường cao hình chóp cụt.
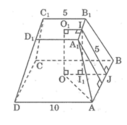
Kẻ A1H ⊥ AB, ta có:
A 1 I = 2,5cm; AJ = 5cm
Suy ra: AH = 2,5cm
Áp dụng định lí Pi-ta-go vào tam giác vuông A 1 H A , ta có:
A 1 A 2 = A 1 H 2 + A H 2 = 52 + 2,52 = 31,25
Suy ra: A 1 A = 31 , 25 ≈ 5,59 (cm)
Ta có: O 1 I = 2,5; OJ = 5cm.
Kẻ I I 1 ⊥ OJ, suy ra I 1 J = 2,5.
Áp dụng định kí Pi-ta-go vào tam giác vuông I I 1 J , ta có:
I J 2 = I I 1 2 + I 1 J 2
Suy ra: I I 1 2 = I J 2 + I 1 J 2 = 52 – 2,52 = 18,75
Suy ra: I I 1 = 18 , 75 ≈ 4,33 (cm)
Vậy O 1 O = I I 1 = 4,33 (cm)
Trong các phát biểu sau, phát biểu nào đúng?
Chiều cao của hình chóp tam giác đều là:
A. độ dài đoạn thẳng nối từ đỉnh của hình chóp tới trung điểm của một cạnh đáy
B. chiều cao của mặt đáy
C. độ dài đường trung tuyến của một mặt bên của hình chóp
D. độ dài đoạn thẳng nối từ đỉnh tới trọng tâm của tam giác đáy.
Cho hình chóp đều S.ABCD có cạnh đáy bằng 4 cm và cạnh bên bằng 3 c m . Cắt hình chóp bởi mặt phẳng (P) song song với mặt phẳng đáy và cách đáy một khoảng 2 cm.
a) Tính chiều cao của hình chóp đều phần chứa đỉnh S sau khi cắt hình chóp đều S.ABCD bởi (P).
b) Tính diện tích một mặt bên hình chóp cụt đều
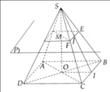
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).
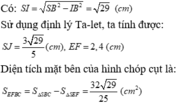
Cho hình chóp cụt tứ giác đều A B C D . A 1 B 1 C 1 D 1 có các cạnh đáy 5cm và 10cm, đường cao mặt bên bằng 5cm. Hãy tính: Diện tích xung quanh của hình chóp cụt.
Diện rích một mặt bên là hình thang bằng:
S =1/2 (5 +10).5=37,5 ( c m 2 )
Diện tích xung quanh của hình chóp
cụt đều là: S x q =4.3,75 = 150 ( c m 2 )
Quan sát hình chóp tứ giác đều ở Hình 3 và cho biết:
a) Mặt đáy và các mặt bên của hình đó.
b) Độ dài cạnh IB
và cạnh BC
c) Đoạn thẳng nào là đường cao của hình đó

a) Mặt đáy: \(ABCD\)
Các mặt bên: \(IAD\); \(IAB\); \(IBC\); \(ICD\)
b) Các cạnh bên bằng nhau: \(IB = IC = 18\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 14\)cm
c) Đoạn thẳng \(IH\) là đường cao của hình chóp
Cho S.ABC là hình chóp tam giác đều có các cạnh bên bằng a và có góc giữa các mặt bên và mặt phẳng đáy là α. Hình nón đỉnh S có đường tròn đáy nội tiếp tam giác đều ABC gọi là hình nón nội tiếp hình nón đã cho. Hãy tính diện tích xung quanh của hình nón này theo a và α
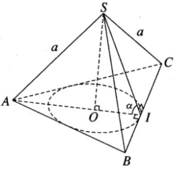
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và

Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy 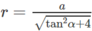
Hình nón nội tiếp có đường sinh là :
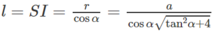
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
![]()