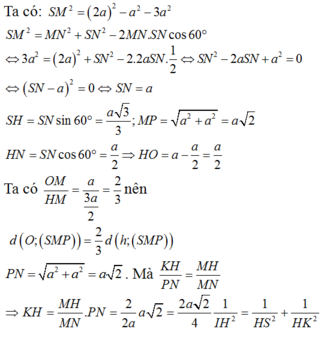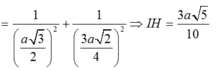Cho hình vuông có cạnh là 7 m tính S hình vuông

Những câu hỏi liên quan
Cho hình vuông có cạnh 10 m
Tính S hình vuông
S hình vuông là:
10x10=100 m2
Đ/s:100 m2
Đúng 0
Bình luận (0)
Bài giải
S hình vuông là :
10 x 10 = 100 ( m2 )
Đáp số : 100 m2
Đúng 0
Bình luận (0)
công thức tính diện tích hình vuông
s = a . a
áp dụng vào bài làm
10.10=100 m2
đáp số...........................
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình vuông cạnh 15 m. Nếu giảm cạnh của hình vuông đi 7 m thì diện tích hình vuông giảm đi bao nhiêu m2 ? diện tính giảm đi là
Xem chi tiết
Lời giải:
Diện tích ban đầu: $15\times 15=225$ (m2)
Nếu giảm cạnh hình vuông đi 7m thì độ dài cạnh mới là: $15-7=8$ (m)
Diện tích lúc sau: $8\times 8=64$ (m2)
Diện tích giảm đi là: $225-64=161$ (m2)
Đúng 2
Bình luận (0)
có 2 cái sân 1 cái hcn 1 cái hình vuông cạnh của sân hình vuông lớn hơn chiều rộng của sân hcn là 7 m và ngắn hơn chiều dài là 4 m .diện tích sân hình vuông lớn hơn diện tích sân hcn là 100 m vuông .Tính cạnh hình vuông.
Gọi a là cạnh của hình vuông (a > 7)
\(\Rightarrow\)
Đúng 0
Bình luận (0)
Xin lỗi nha
Gọi a là cạnh hình vuông (a>7)
=> chiều dài hcn là a+4 m
chiều rộng hcn là a-7 m
Theo đề ra ta có a2-100 =(a-7)(a+4)
<=>a2-100=a2-7a+4a-28
<=> 3a=72
<=>a=24
Vậy.....
Đúng 0
Bình luận (0)
Hình vuông AEBF có cạnh bằng 1m,hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF A) tính S của hình vuông ABCD B) Tính độ dài đường chéo AB
a: ABCD là hình vuông
=>AB=BC=CD=DA và \(\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{ADC}=90^0\) và AC là phân giác của \(\widehat{DAB}\) và DB là phân giác của góc ADC; BD là phân giác của góc ABC
AC là phân giác của góc DAB
=>\(\widehat{CAB}=\dfrac{1}{2}\widehat{DAB}=\dfrac{1}{2}\cdot90^0=45^0\)
AEBF là hình vuông
=>AB là phân giác của \(\widehat{FAE}\) và \(\widehat{FAE}=90^0\)
=>\(\widehat{BAE}=\dfrac{1}{2}\cdot\widehat{EAF}=45^0\)
\(\widehat{BAE}=45^0\)
\(\widehat{BAC}=45^0\)
Do đó: \(\widehat{BAE}=\widehat{BAC}=45^0\)
=>AE và AC là hai tia trùng nhau
=>A,E,C thẳng hàng
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
AEBF là hình vuông
=>BA là phân giác của góc EBF
=>\(\widehat{ABE}=\dfrac{1}{2}\cdot\widehat{FBE}=45^0\)
=>\(\widehat{ABE}=\widehat{ABD}\)
=>BE,BD là hai tia trùng nhau
=>B,E,D thẳng hàng
B,E,D thẳng hàng
A,E,C thẳng hàng
Do đó: BD cắt AC tại E
ADCB là hình vuông
=>AC=BD và AC vuông góc với BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại E và E là trung điểm chung của AC và DB
E là trung điểm của AC nên AC=2AE=2(cm)
E là trung điểm của BD nên BD=2EB=2(cm)
Xét tứ giác ADCB có DB\(\perp\)AC
nên \(S_{ADCB}=\dfrac{1}{2}\cdot DB\cdot AC=\dfrac{1}{2}\cdot2\cdot2=2\left(cm^2\right)\)
b: ADCB là hình vuông
=>\(S_{ADCB}=AB^2\)
=>\(AB^2=2\)
=>\(AB=\sqrt{2}\left(cm\right)\)
Đúng 2
Bình luận (0)
cho hình vuông ABCD ,M thuộc đường chéo AC.Gọi E,F theo thứ tự là hình chiếu của M trên AD,CD.Cmr
a) BM vuông góc với EF
b) các đường thẳng BM,AF,CE đồng quy
c) Tính S bef biết hình vuông có cạnh bằng 7 cm, AM=3 căn 2 cm
bạn xem ở đây có 2 ý đầu đấy http://d.violet.vn//uploads/resources/624/3367194/preview.swf
Đúng 0
Bình luận (0)
Câu 1 : Một hình chữ nhật có chiều dài 53m, chiều rộng 36m được chia thành những hình vuông có S bằng nhau.Tính chiều dài cạnh hình vuông lớn nhất trong cách chia trên(số đo cạnh là số tự nhiên với đơn vị là m)Câu 2 : Một hình chữ nhật có chiều dài 105m và rộng 75m được chia thành các hình vuông có S nhau. Tính độ dài cạnh hình vuông lớn nhất trong cách chia trên(số đo cạnh là số tự nhiên với đơn vị là m)
Đọc tiếp
Câu 1 : Một hình chữ nhật có chiều dài 53m, chiều rộng 36m được chia thành những hình vuông có S bằng nhau.Tính chiều dài cạnh hình vuông lớn nhất trong cách chia trên(số đo cạnh là số tự nhiên với đơn vị là m)
Câu 2 : Một hình chữ nhật có chiều dài 105m và rộng 75m được chia thành các hình vuông có S = nhau. Tính độ dài cạnh hình vuông lớn nhất trong cách chia trên(số đo cạnh là số tự nhiên với đơn vị là m)
Câu 1:
Chiều dài cạnh hình vuông lớn nhất là ƯCLN(53, 36) với đơn vị là m. Mà ƯCLN(53, 36) = 1 nên chiều dài cạnh hình vuông lớn nhất là 1m
Đúng 3
Bình luận (0)
Chiều dài cạnh hình vuông lớn nhất là ƯCLN(53, 36) với đơn vị là m. Mà ƯCLN(53, 36) = 1 nên chiều dài cạnh hình vuông lớn nhất là 1m
Đúng 0
Bình luận (0)
cho hình chóp s.abcd có đáy abcd là hình vuông cạnh a, \(SA=\sqrt{7}\) và vuông góc với đáy. lấy điểm M trên cạnh SC sao cho CM < a. gọi (C) là hình nón có đỉnh C, các điểm B, M, D thuộc mặt xung quanh, điểm A thuộc mặt đáy của hình nón. tính diện tích xung quanh của (C)
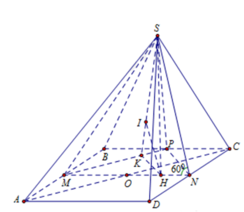
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng
60
0
. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 0 . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
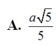
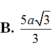
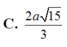
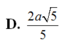
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng
60
°
. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC A.
a
5
5
B.
5
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 3
D. 2 a 5 5