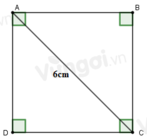
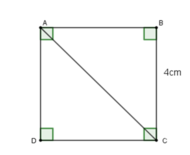
a: ABCD là hình vuông
=>AB=BC=CD=DA và \(\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{ADC}=90^0\) và AC là phân giác của \(\widehat{DAB}\) và DB là phân giác của góc ADC; BD là phân giác của góc ABC
AC là phân giác của góc DAB
=>\(\widehat{CAB}=\dfrac{1}{2}\widehat{DAB}=\dfrac{1}{2}\cdot90^0=45^0\)
AEBF là hình vuông
=>AB là phân giác của \(\widehat{FAE}\) và \(\widehat{FAE}=90^0\)
=>\(\widehat{BAE}=\dfrac{1}{2}\cdot\widehat{EAF}=45^0\)
\(\widehat{BAE}=45^0\)
\(\widehat{BAC}=45^0\)
Do đó: \(\widehat{BAE}=\widehat{BAC}=45^0\)
=>AE và AC là hai tia trùng nhau
=>A,E,C thẳng hàng
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
AEBF là hình vuông
=>BA là phân giác của góc EBF
=>\(\widehat{ABE}=\dfrac{1}{2}\cdot\widehat{FBE}=45^0\)
=>\(\widehat{ABE}=\widehat{ABD}\)
=>BE,BD là hai tia trùng nhau
=>B,E,D thẳng hàng
B,E,D thẳng hàng
A,E,C thẳng hàng
Do đó: BD cắt AC tại E
ADCB là hình vuông
=>AC=BD và AC vuông góc với BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại E và E là trung điểm chung của AC và DB
E là trung điểm của AC nên AC=2AE=2(cm)
E là trung điểm của BD nên BD=2EB=2(cm)
Xét tứ giác ADCB có DB\(\perp\)AC
nên \(S_{ADCB}=\dfrac{1}{2}\cdot DB\cdot AC=\dfrac{1}{2}\cdot2\cdot2=2\left(cm^2\right)\)
b: ADCB là hình vuông
=>\(S_{ADCB}=AB^2\)
=>\(AB^2=2\)
=>\(AB=\sqrt{2}\left(cm\right)\)