Mai em thi rồi, ai giúp em giải bài 3 với ạ :((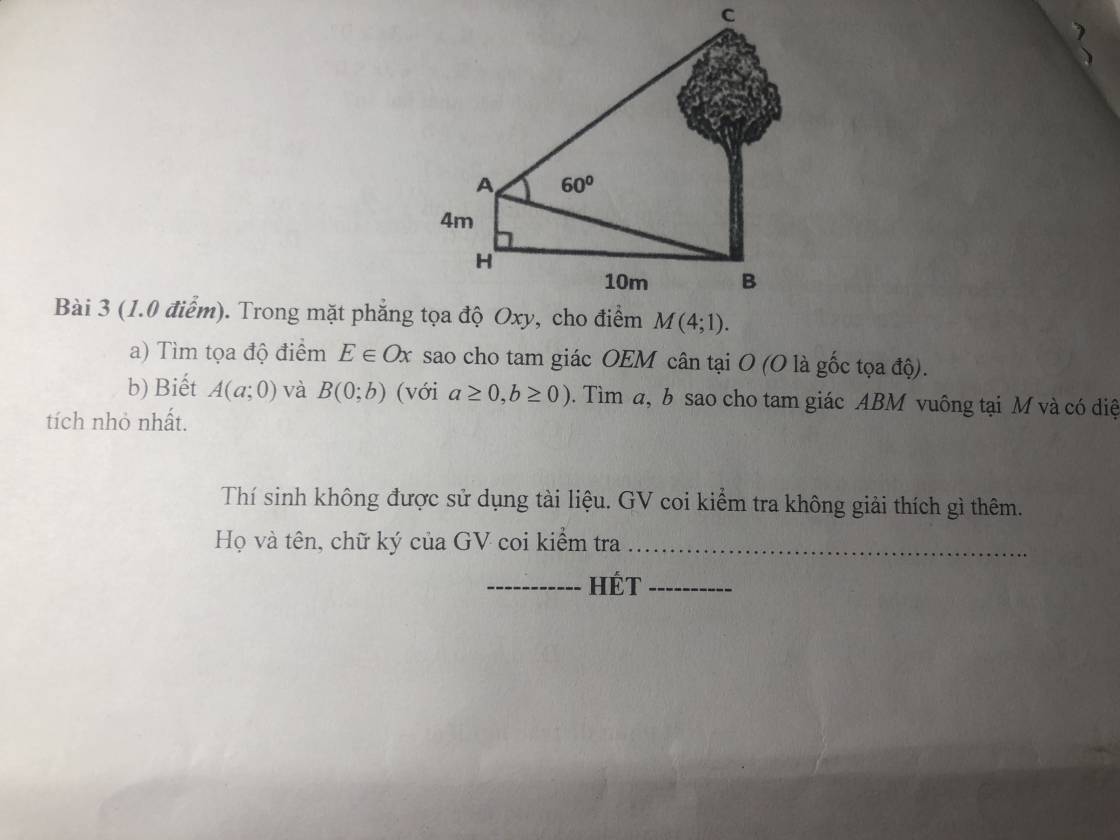

Những câu hỏi liên quan
Ai giúp em giải bài này với ạ, mai em thi rồi ^^

2.
Gọi \(H\left(x;y\right)\) là toạ độ chân đường cao ứng với BC \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x-1;y+2\right)\\\overrightarrow{BC}=\left(2;1\right)\end{matrix}\right.\)
Do AH vuông góc BC \(\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow2\left(x-1\right)+y+2=0\Leftrightarrow y=-2x\)
\(\Rightarrow H\left(x;-2x\right)\Rightarrow\overrightarrow{BH}=\left(x+2;-2x-3\right)\)
Do H thuộc BC nên B, C, H thẳng hàng hay các vecto \(\overrightarrow{BC};\overrightarrow{BH}\) cùng phương
\(\Rightarrow\dfrac{x+2}{2}=\dfrac{-2x-3}{1}\Rightarrow x=\dfrac{8}{5}\Rightarrow y=-\dfrac{16}{5}\) \(\Rightarrow H\left(-\dfrac{8}{5};\dfrac{16}{5}\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(-\dfrac{13}{5};\dfrac{26}{5}\right)\Rightarrow\left\{{}\begin{matrix}AH=\sqrt{\left(-\dfrac{13}{5}\right)^2+\left(-\dfrac{6}{5}\right)^2}=\dfrac{13\sqrt{5}}{5}\\BC=\sqrt{2^2+1^2}=\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{13}{2}\)
Đúng 1
Bình luận (0)
3.
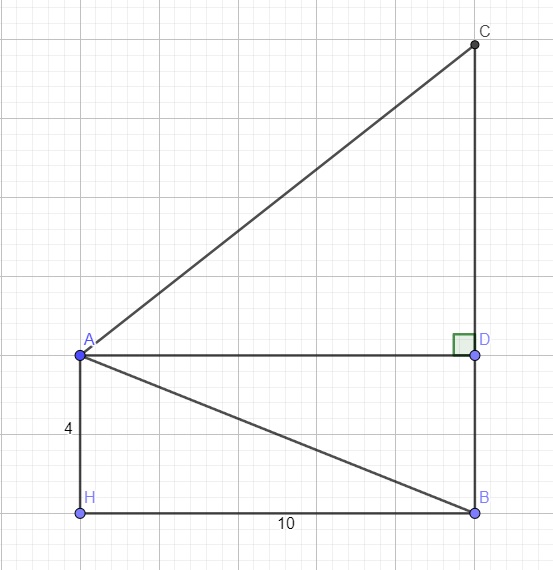
Kẻ AD vuông góc BC tại D
\(\Rightarrow AD=BH=10\) ; \(BD=AH=4\)
\(tan\widehat{BAD}=\dfrac{BD}{AD}=\dfrac{2}{5}\Rightarrow\widehat{BAD}\approx21^048'5''\)
\(\Rightarrow\widehat{CAD}=60^0-\widehat{BAD}=38^011'55''\)
\(\Rightarrow CD=AD.tan\widehat{CAD}=7,87\left(m\right)\)
\(\Rightarrow BC=BD+CD=11,87\left(m\right)\)
Đúng 1
Bình luận (0)
mai thi rồi ai giúp em giải bài này với ạ
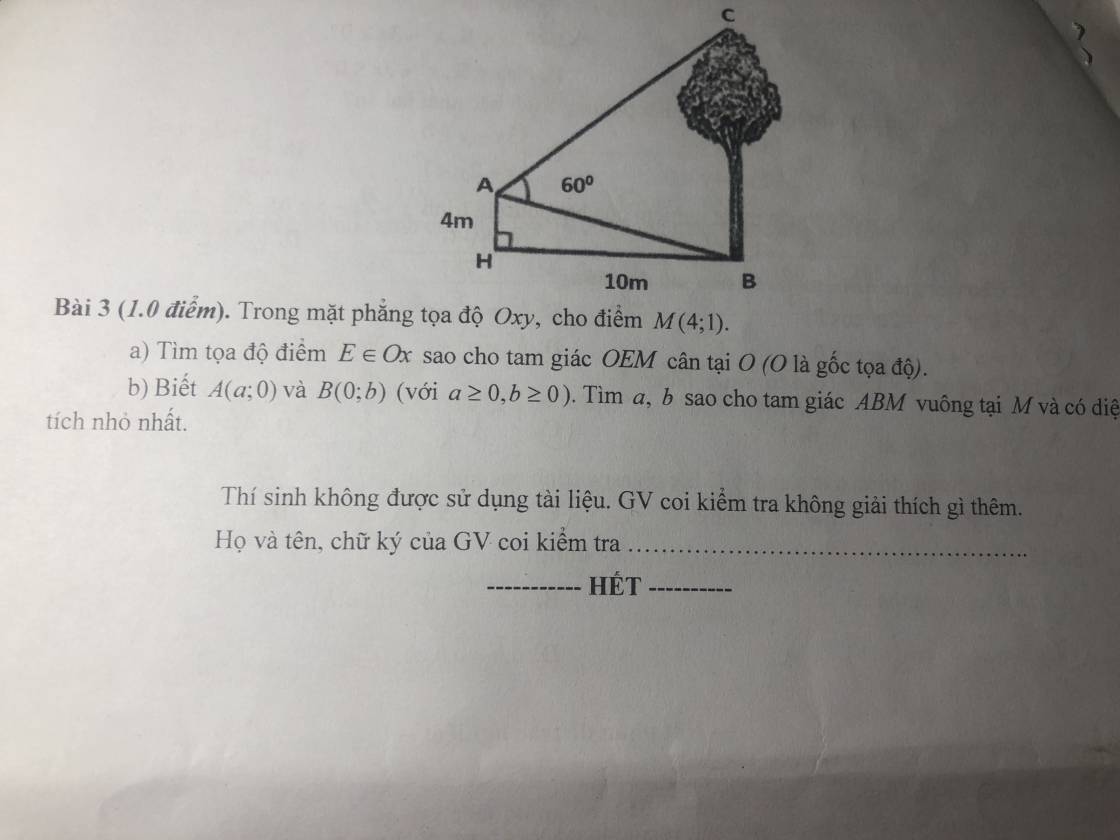
a.
D E thuộc Ox \(\Rightarrow\) tọa độ E có dạng \(E\left(x;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OE}=\left(x;0\right)\\\overrightarrow{OM}=\left(4;1\right)\end{matrix}\right.\)
Tam giác OEM cân tại O \(\Rightarrow OE=OM\)
\(\Rightarrow\sqrt{x^2+0^2}=\sqrt{4^2+1^2}\Rightarrow x^2=17\)
\(\Rightarrow x=\pm\sqrt{17}\Rightarrow\left[{}\begin{matrix}E\left(\sqrt{17};0\right)\\E\left(-\sqrt{17};0\right)\end{matrix}\right.\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{MA}=\left(a-4;-1\right)\\\overrightarrow{MB}=\left(-4;b-1\right)\end{matrix}\right.\)
Tam giác ABM vuông tại M \(\Rightarrow\overrightarrow{MA}.\overrightarrow{MB}=0\)
\(\Rightarrow-4\left(a-4\right)-1\left(b-1\right)=0\)
\(\Leftrightarrow4a+b-17=0\Rightarrow b=17-4a\)
Lại có \(S_{ABM}=\dfrac{1}{2}MA.MB=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{\left(b-1\right)^2+16}\)
\(=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{\left(16-4a\right)^2+16}=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{16\left[\left(a-4\right)^2+1\right]}\)
\(=2\left[\left(a-4\right)^2+1\right]\ge2\)
Dấu "=" xảy ra khi \(a-4=0\Rightarrow a=4\Rightarrow b=1\)
Đúng 1
Bình luận (0)
Mn giúp em giải với ạ, em cần gấp để ôn ngày mai em thi rồi ạ! Mong mn giúp em
1 The distance from my home to school is about 3 km
2 My mum used to live in a small village when she was small
3 Despite being a millionaire , he lives in a small flat
4 when does the festive take place ?
5 It is about two kilometres from my home to school
6 he didn't use to ride his bike to school
7 Despite having a test tomrrow , they are still watching TV now
Đúng 1
Bình luận (0)
Viết một đoạn văn quy nạp phân tích bài thơ "Tức cảnh Pắc Pó" của Hồ Chí Minh
AI GIÚP EM VỚI Ạ MAI EM THI RỒI
Mn giúp em bài 11c và bài 4f với ạ mai em nộp rồi
Riêng bài 4f thì em có tìm được 1 dạng giải nhưng khó hiểu quá, ai có cách nào dễ hiểu hơn thì giúp em với

11c.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{16a-b^2}{4a}=\dfrac{9}{2}\\16a+4b+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b^2=-4a\\b=-4a-1\end{matrix}\right.\)
\(\Rightarrow2b^2-b=1\Leftrightarrow2b^2-b-1=0\Rightarrow\left[{}\begin{matrix}b=1\Rightarrow a=-\dfrac{1}{2}\\b=-\dfrac{1}{2}\Rightarrow a=-\dfrac{1}{8}\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=-\dfrac{1}{2}x^2+x+4\\y=-\dfrac{1}{8}x^2-\dfrac{1}{2}x+4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
4f.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}1+b+c=0\\\dfrac{4c-b^2}{4}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-b-1\\c=\dfrac{b^2}{4}-1\end{matrix}\right.\)
\(\Rightarrow\dfrac{b^2}{4}+b=0\)
\(\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow c=-1\\b=-4\Rightarrow c=3\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=x^2-1\\y=x^2-4x+3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
ai giải giúp mik bài 4 với ạ mai mik thi rồi á
a. Trọng lượng của vật là:
P=10.m= 10.15=150N
Trọng lực có phương thẳng đứng, chiều từ trên xuống dưới. b.
b. 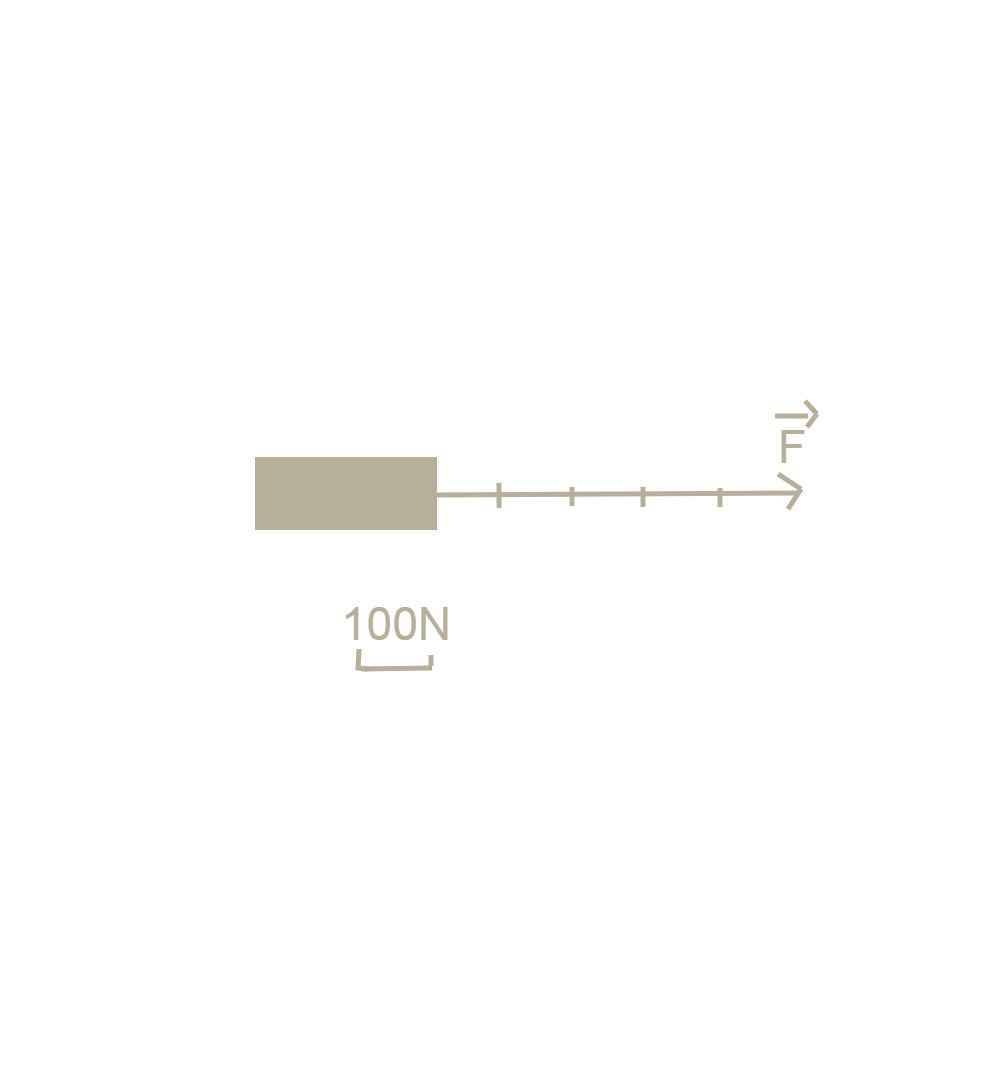 c.Trọng lượng của vật là:
c.Trọng lượng của vật là:
P= 10.m= 10.6=60N
Trọng lượng có phương thẳng, đứng chiều từ trên xuống dưới.
Vì vật đang đứng yên, nên chứng tỏ đã có 2 lực cân bằng tác dụng vào vật. Đó là trọng lực và lực nâng (P = Q)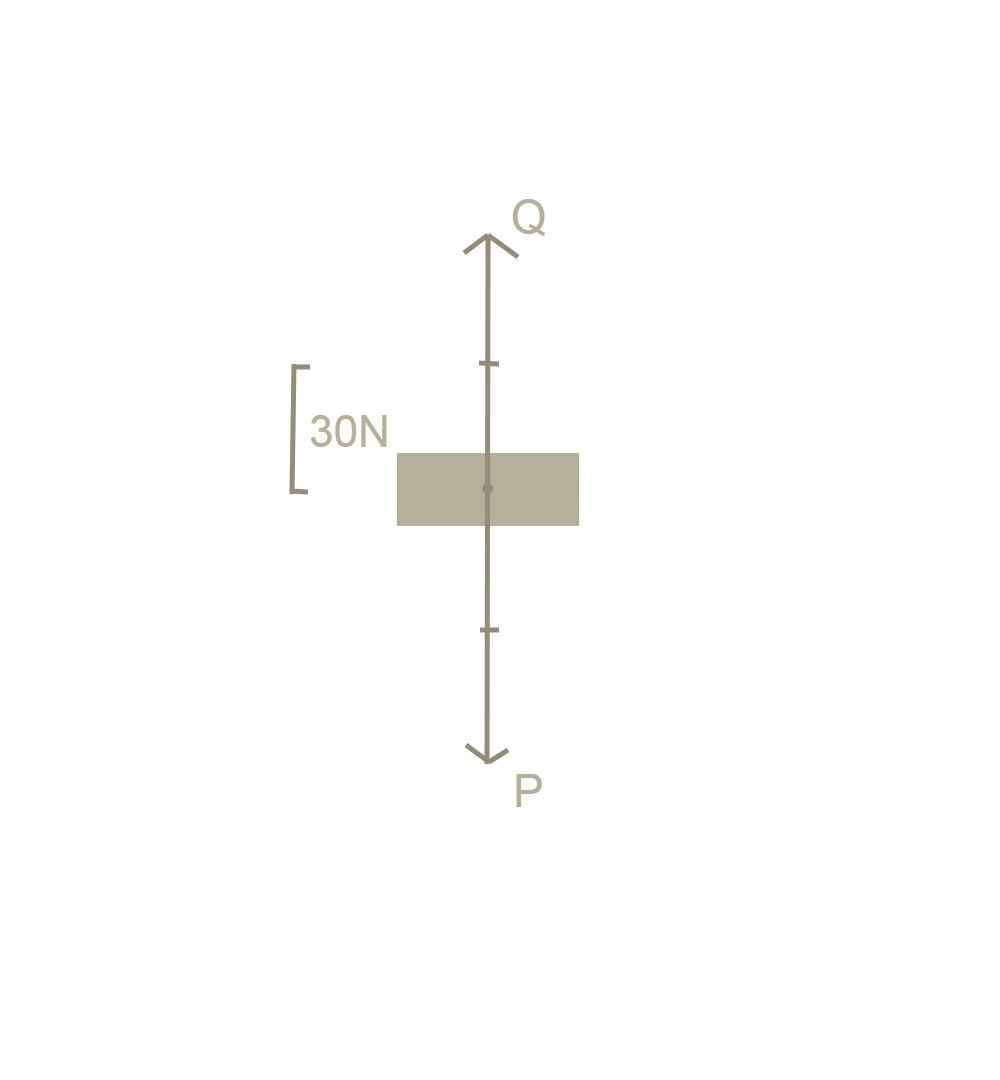
Đúng 0
Bình luận (0)

Mọi người giải giúp em với ạ, mai em thi rồi, mấy anh/chị giải thích rõ ràng giùm em nhé, em cảm ơn ạ.
Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)
Đúng 0
Bình luận (1)
17:
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}-1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2+1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2\in\left\{1;-1\right\}\)
=>\(\sqrt{x}\in\left\{3;1\right\}\)
=>\(x\in\left\{9;1\right\}\)
16:
a: BC=BH+CH
=9+16
=25(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{9\cdot25}=15\left(cm\right)\\AC=\sqrt{16\cdot25}=20\left(cm\right)\end{matrix}\right.\)
b: M là trung điểm của AC
=>AM=AC/2=10(cm)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\dfrac{15}{10}=\dfrac{3}{2}\)
nên \(\widehat{AMB}\simeq56^0\)
Đúng 0
Bình luận (0)
Anh chị giúp em với ạ, mai em thi rồi mà chưa có giải xong đề cương
Bài 8:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó:ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M
Đúng 1
Bình luận (0)
 ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ
ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ















