Cho \(\Delta ABC\)có \(\widehat{A}\)=90 độ . \(\widehat{B}\)=30 độ AB=3cm . Tính AC,BC

Những câu hỏi liên quan
Cho Delta ABC có widehat{A} 90 độ, vẽ tia phân giác widehat{C} cắt AB ở H. Lấy E inBC sao cho CA CEa) Chứng minh DeltaCAH DeltaCEH và HE perp BCb) Kẻ EK perp AC tại K, EK cắt CH tại I. Chứng minh widehat{HEI}-widehat{HAI}c) Chứng minh HE // AI và widehat{AIE}-widehat{ABC} 90 độ
Đọc tiếp
Cho \(\Delta ABC\) có \(\widehat{A}\)= 90 độ, vẽ tia phân giác \(\widehat{C}\) cắt AB ở H. Lấy E \(\in\)BC sao cho CA = CE
a) Chứng minh \(\Delta\)CAH = \(\Delta\)CEH và HE \(\perp\) BC
b) Kẻ EK \(\perp\) AC tại K, EK cắt CH tại I. Chứng minh \(\widehat{HEI}-\widehat{HAI}\)
c) Chứng minh HE // AI và \(\widehat{AIE}-\widehat{ABC}\)= 90 độ
cho \(\Delta ABC\)có góc A=90 độ BA<AC trên AC lấy D sao cho AD=AB trên tia đối AB lấy E sao cho AE=AC
CMR
a)DE=BC
b)DE \(\perp\)BC
c)\(4\widehat{B}\)=\(5\widehat{C}\)Tính \(\widehat{AED}\)
a) xét \(\Delta ADE\) và \(\Delta ABC\) có
\(AD=AB\)
\(AE=AC\)
\(\widehat{BAC}=\widehat{DAE}=90^0\)
\(\Rightarrow\Delta ABC=\Delta ADE\left(c.g.c\right)\)
\(\Rightarrow DE=BC\) ( 2 cạnh tương ứng = nhau)
Đúng 0
Bình luận (0)
Cho △ABC có \(\widehat{A}\)=45 độ, \(\widehat{B}\)=75 độ thì:
a. BC<AB<AC
b. BC<AC<AB
c. AB<AC<BC
d. AC<BC<AB
Xem thêm câu trả lời
Cho \(\Delta ABC\) có \(\widehat{A}\) = 90 độ. AB = AC. Qua A kẻ đường thẳng xy cắt đoạn thẳng BC. Kẻ BM và CN \(\perp xy\). Chứng minh MN = BM - CN
\(\Delta ABC\) có \(\widehat{A}=105^0,\widehat{B}=45^0,BC=4cm\) . Tính độ dài cạnh AB, AC.
Cho Hình 4.20, biết \(AB = CB, AD = CD,\widehat{DAB} = {90^\circ },\widehat{BDC} = {30^\circ }\)
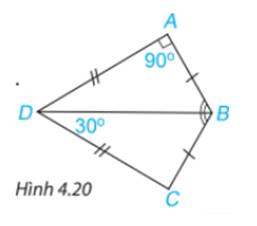
a) Chứng minh rằng \(\Delta ABD = \Delta CBD\).
b) Tính \(\widehat {ABC}\).
a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)
Đúng 0
Bình luận (0)
Cho Delta ABCcówidehat{ABC}55^o, trên cạnh AC lấy điểm D (D ko trùng với A và C)a. Tính độ dài AC, biết AD4cm, CD3cm.b. Tính số đo củawidehat{DBC}, biết widehat{ABD}30^o.c. Từ B dựng tia Bx sao cho widehat{DBx}90^o. Tính số đo widehat{ABx}(Với số đo các góc theo câu b.)d. Trên cạnh AB lấy điểm E (E ko trùng với A và B). Chứng minh rằng 2 đoạn thẳng BD và CE cắt nhau.
Đọc tiếp
Cho \(\Delta ABC\)có\(\widehat{ABC}=55^o\), trên cạnh AC lấy điểm D (D ko trùng với A và C)
a. Tính độ dài AC, biết AD=4cm, CD=3cm.
b. Tính số đo của\(\widehat{DBC}\), biết \(\widehat{ABD}=30^o\).
c. Từ B dựng tia Bx sao cho \(\widehat{DBx}=90^o\). Tính số đo \(\widehat{ABx}\)(Với số đo các góc theo câu b.)
d. Trên cạnh AB lấy điểm E (E ko trùng với A và B). Chứng minh rằng 2 đoạn thẳng BD và CE cắt nhau.
Giải \(\Delta\)vuông ABC biết \(\widehat{A}\)=90 độvà
a, AC=20 cm, \(\widehat{B}\)= 48 độ
b, AC= 15 cm, \(\widehat{C}\)= 30 độ
c, AC= 21 cm, AB= 18 cm
Hai tam giác ABC và tam giác MNP có A^=M^;B^=N^;AB=3cm,MN=5cm.\widehat{A}=\widehat{M};\widehat{B}=\widehat{N};AB=3cm,MN=5cm.A=M;B=N;AB=3cm,MN=5cm. Tính độ dài cạnh BC và NP, biết tổng của chúng là 24cm.

















