Cho $\triangle ABC$ có trọng tâm $G$. Vẽ đường thẳng $d$ qua $G$ và song song với $AB$, $d$ cắt $BC$ tại điểm $M$. Chứng minh rằng $B M=\dfrac{1}{3} B C$.

Những câu hỏi liên quan
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \dfrac{1}{3}BC\)
Lấy D là trung điểm của cạnh BC.
Khi đó, AD là đường trung tuyến của tam giác ABC.
Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.
Ta có \(\dfrac{{AG}}{{A{\rm{D}}}} = \dfrac{2}{3}\) hay \(AG = \dfrac{2}{3}A{\rm{D}}\)
Vì MG // AB, theo định lí Thalès, ta suy ra: \(\dfrac{{AG}}{{A{\rm{D}}}} = \dfrac{{BM}}{{B{\rm{D}}}} = \dfrac{2}{3}\)
Ta có BD = CD (vì D là trung điểm của cạnh BC) nên \(\dfrac{{BM}}{{BC}} = \dfrac{{BM}}{{2B{\rm{D}}}} = \dfrac{2}{{2.3}} = \dfrac{1}{3}\)
Do đó \(BM = \dfrac{1}{3}BC\) (đpcm).
Đúng 0
Bình luận (0)
Cho G là trọng tâm của tam giác ABC. Qua G vẽ đường thẳng song song với AB cắt BC tại D. Chứng minh rằng BD=\(\dfrac{1}{3}\)BC.
Gọi E là trung điểm của AB
Xét ΔABC có
CE là đường trung tuyến ứng với cạnh AB(E là trung điểm của AB)
G là trọng tâm của ΔABC(Gt)
Do đó: G∈CE(Tính chất ba đường trung tuyến của tam giác)
⇒GD//BE
Xét ΔABC có
CE là đường trung tuyến ứng với cạnh AB(E là trung điểm của AB)
G là trọng tâm của ΔABC(gt)
Do đó: \(CG=\dfrac{2}{3}CE\)(Tính chất ba đường trung tuyến của tam giác)(1)
Ta có: CG+GE=CE(G nằm giữa C và E)
⇔GE=CE-EG
hay \(GE=\dfrac{1}{3}CE\)(2)
Từ (1) và (2) suy ra \(\dfrac{CG}{GE}=\dfrac{2}{1}\)
Xét ΔCEB có
G∈CE(cmt)
D∈BC(gt)
GD//EB(cmt)
Do đó: \(\dfrac{GC}{EG}=\dfrac{DC}{BD}\)(Định lí Ta lét)
⇒\(\dfrac{DC}{BD}=2\)
hay DC=2BD
Ta có: BD+DC=BC(D nằm giữa B và C)
⇔2BD+BD=BC
⇔3BD=BC
hay \(BD=\dfrac{1}{3}BC\)(đpcm)
Đúng 5
Bình luận (0)
Từ điểm C kẻ đường trung tuyến CE của tam giác ABC
Ta có GD sog sog AB (gt).
Suy ra : GD sog sog BE ( E thuộc AB)
Xét Tam giác ABC: G là trọng tâm (gt)
Suy ra: GE/CE = 1/3 (Tc trọng tâm trong tgiác)
Xét tam giác BCE có: GD sog sog BE (cmt)
Suy ra: BD/BC = GE/CE (định lý Talet)
mà: GE/CE = 1/3 (cmt)
Suy ra: BD = 1/3 BC (đpcm)
Đúng 2
Bình luận (0)
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD AB. Lấy G thuộc cạnh AC sao cho
A
G
1
3
A
C
. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.Chứng minh:a) G là trọng tâm tam giác BCD;b)
∆
B
E
D
∆...
Đọc tiếp
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Lấy G thuộc cạnh AC sao cho A G = 1 3 A C . Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.
Chứng minh:
a) G là trọng tâm tam giác BCD;
b) ∆ B E D = ∆ F D E , từ đó suy ra EC = DF;
c) ∆ D M F = ∆ C M E ;
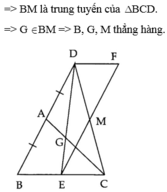
d) B, G, M thẳng hàng.
Bài 3.Cho ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Lấy G thuộc cạnh AC sao cho AG = 1 3 AC. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.Chứng minh:
a) G là trọng tâm BCD;
b) EC = DF
c) DMF = CME;
d) B, G, M thẳng hàng.
cho tam giác ABC, trung tuyến AD, gọi G là trọng tâm ABC đường thẳng d đi qua G cắt AB, AC tại M và N. Qua B và C kẻ các đường thẳng song song với d cắt AD ở B và C. chứng minh rằng����+����3AMAB+ANAC3 VÀ ����+����1AMBM+ANCN1
Đọc tiếp
cho tam giác ABC, trung tuyến AD, gọi G là trọng tâm ABC đường thẳng d đi qua G cắt AB, AC tại M và N. Qua B và C kẻ các đường thẳng song song với d cắt AD ở B' và C'. chứng minh rằng
VÀ
Cho ∆ABC, vẽ các đường thẳng a đi qua A và song song với BC, b đi qua B và song song với AC, c đi qua C và song song với AB. a cắt b tại E, b cắt c tại D, c cắt A tại F.
a. Chứng minh rằng AD, BF, CE cùng đi qua 1 điểm.
b. Chứng minh rằng trọng tâm của 2 ∆ ABC và DEF trùng nhau.
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Lấy G thuộc cạnh AC sao cho AG = AC. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD. Chứng minh: a) G là trọng tâm tam giác BCD. b) , từ đó suy ra EC = DF
Cho tam giác ABC có AM là đường trung tuyến, G là trọng tâm. Qua G vẽ đường thẳng song song với AB cắt BC ở D, qua G vẽ đường thẳng song song với AC cắt BC ở E. Chứng minh rằng: A:BD/BM=2/3 B:BD=DE=EC
cho tam giác ABC trên tia đối của AB lấy D sao cho AD = AB . Lấy G thuộc AC sao cho AG =1/3 AC . Tia DG cắt BC tại E . Qua E vẽ đường thẳng song song với BD . Qua D vẽ dường thảng song song với BC 2 đường này cắt nhau tại F gọi M là giao điểm của EF vsf CD
a)chứng minh G là trọng tâm của tam giác BCD
b)chứng minh tam giác BED = tam giác FDE