\(a,12\left(x-1\right)=0\\ x-1=0\\ x=1\\ b,45+5\left(x-3\right)=70\\ 5\left(x-3\right)=25\\ x-3=5\\ x=8\\ c,3.x-18:2=12\\ 3.x-9=12\\ 3.x=21\\ x=7\)

12(x-1)=0

     (x-1)=0:12

      x-1=0

      x=0+1

      x= 1

Vậy x= 1

12 ( x - 1 ) = 0
       x - 1   = 0 : 12
       x - 1   = 0
=>   x        = 1

Ta nhận thấy tổng các hệ số trong phương trình đã cho là 

\(1-2\left(m-1\right)+2m-3=0\) nên pt này luôn có 1 nghiệm bằng 1, còn nghiệm kia là \(2m-3\). Do vai trò của \(x_1,x_2\) trong \(x^2+2x_1x_2-x_2=1\) là không như nhau nên ta phải chia làm 2TH:

 TH1: \(x_1=1;x_2=2m-3\). Khi đó ta có 

\(1+2\left(2m-3\right)-\left(2m-3\right)=1\) \(\Leftrightarrow2m-3=0\) \(\Leftrightarrow m=\dfrac{3}{2}\)

 TH2: \(x_1=2m-3;x2=1\). Khi đó

\(\left(2m-3\right)^2+2\left(2m-3\right)-1=1\) \(\Leftrightarrow4m^2-8m+1=0\) \(\Leftrightarrow m=\dfrac{2\pm\sqrt{3}}{2}\)

Vậy để pt đã cho có 2 nghiệm \(x_1,x_2\) thỏa ycbt thì \(\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=\dfrac{2\pm\sqrt{3}}{2}\end{matrix}\right.\)

Ta thấy các hệ số \(a,b,c\) của phương trình đã cho thỏa mãn \(a-b+c=1-\left[-\left(m-3\right)\right]-m+2=1+m-3-m+2=0\)

nên phương trình đã cho sẽ có một nghiệm là \(-1\) và nghiệm kia là \(m-2\).

Trong hệ thức \(x_1^2+x_2=8\), vai trò của \(x_1,x_2\) không như nhau nên ta xét 2 trường hợp:

TH1: Nếu \(x_1=-1\) thì \(x_1^2+x_2=8\Leftrightarrow\left(-1\right)^2+m-2=8\Leftrightarrow m=9\).

TH2: Nếu \(x_2=-1\) thì \(x_1^2+x_2=8\Leftrightarrow\left(m-2\right)^2-1=8\Leftrightarrow\left(m-2\right)^2=9\) \(\Leftrightarrow m-2=\pm3\) \(\Leftrightarrow\left[{}\begin{matrix}m=5\\m=-1\end{matrix}\right.\). 

Vậy để phương trình đã cho có 2 nghiệm thỏa điều kiện đề cho thì \(\left[{}\begin{matrix}m=-1\\m=5\\m=9\end{matrix}\right.\)

Lời giải:
Để pt có 2 nghiệm thì $\Delta=(m-3)^2-4(-m+2)\geq 0$

$\Leftrightarrow (m-1)^2\geq 0$ (luôn đúng với mọi $m\in\mathbb{R}$)

Áp dụng định lý Viet:

$x_1+x_2=m-3$

$x_1x_2=-m+2$

$\Rightarrow x_1+x_2+x_1x_2=-1$

$\Leftrightarrow x_1+x_2+x_1x_2+1=0$

$\Leftrightarrow (x_1+1)(x_2+1)=0$

$\Leftrightarrow x_1=-1$ hoặc $x_2=-1$

TH1: $x_1=-1$

$x_2=\frac{-m+2}{x_1}=m-2$. Khi đó:
$x_1^2+x_2=8$

$\Leftrightarrow (-1)^2+(m-2)=8$

$\Leftrightarrow m=9$

TH2: $x_2=-1$

$x_1=\frac{-m+2}{x_2}=m-2$. Khi đó:
$x_1^2+x_2=8$

$\Leftrightarrow (m-2)^2-1=8$

$\Leftrightarrow (m-2)^2=9$

$\Leftrightarrow m-2=\pm 3\Leftrightarrow m=5$ hoặc $m=-1$

Trước hết ta xét ĐK của m để pt có hai nghiệm phân biệt

Ta có : Δ = b² - 4ac = ( 2m - 3 )² - 4( -2m + 2 )

= 4m² - 12m + 9 + 8m - 8

= 4m² - 4m + 1 = ( 2m - 1 )² > 0 ∀ m ≠ 1/2

Vậy ∀ m ≠ 1/2 thì pt có hai nghiệm phân biệt

Theo hệ thức Viète ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-2m+3\\x_1x_2=\dfrac{c}{a}=-2m+2\end{matrix}\right.\)

Khi đó x₁² + x₂² = 17

<=> ( x₁ + x₂ )² - 2x₁x₂ - 17 = 0

<=> ( -2m + 3 )² - 2( -2m + 2 ) - 17 = 0

<=> 4m² - 12m + 9 + 4m - 4 - 17 = 0

<=> 4m² - 8m - 12 = 0

<=> m² - 2m - 3 = 0

<=> ( m - 3 )( m + 1 ) = 0

<=> m = 3 hoặc m = -1 (tm)

=> Chọn A.2

c) Theo định lí Vi-et ta có:

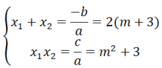
P = x 1 2 + x 2 2  = (x1 + x2 )2 - 2 x 1 x 2  = 4 m + 3 2  - 2( m 2  + 3)

= 4( m 2  + 6m + 9) - 2( m 2  + 3) = 2 m 2  + 24m + 30

\(2^3x+5^2x=2.\left(5^2+2^3\right)-33\)

\(8x+25x=2.\left(25+8\right)-33\)

\(8x+25x=2.33-33\)

\(8x+25x=66-33\)

\(8x+25x=33\)

\(x+\left(8+25\right)=33\)

\(x+33=33\)

\(x=0\)

\(15:\left(x+2\right)=\left(3^3+3\right):10\)

\(15:\left(x+2\right)=\left(27+3\right):10\)

\(15:\left(x+2\right)=30:10\)

\(15:\left(x+2\right)=3\)

\(x+2=15:3\)

\(x+2=5\)

\(x=3\)

Ta có: \(15:\left(x+2\right)=\left(3^3+3\right):10\)

\(\Leftrightarrow15:\left(x+2\right)=3\)

\(\Leftrightarrow x+2=5\)

hay x=3