Bài 3 Cho tam giác ABC và cân tại A đường cao AH gọi k là điểm đối xứng của H Qua AB: CM tứ giác AHBK la hình vuông B H C

Những câu hỏi liên quan
Cho Tam giác abc vg cân tại a đường cao ah gọi k là điểm đối xứng của h qua ab cm tứ giác ahbk là hvg
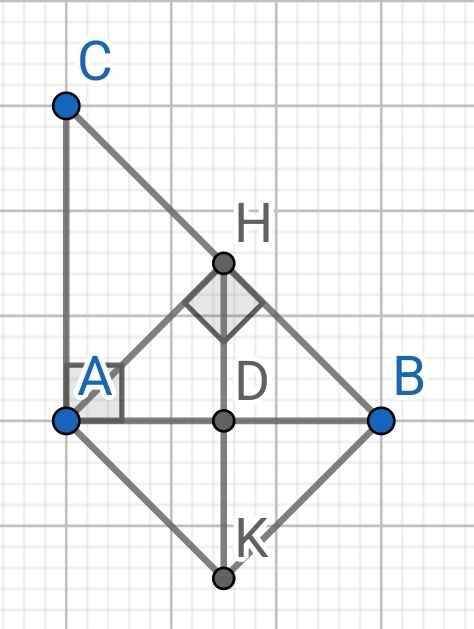
Do AH ⊥ BC (gt)
⇒ AH ⊥ BH
Do ∆ABC vuông cân tại A (gt)
AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm của BC
Gọi D là giao điểm của AB và HK
Do H và K đối xứng nhau qua AB (gt)
⇒ D là trung điểm của HK và AB là đường trung trực của HK
⇒ HK ⊥ AB
Mà AB ⊥ AC
⇒ HK // AC
⇒ HD // AC
Mà H là trung điểm của BC
⇒ D là trung điểm AB
Do ∆ABC vuông cân tại A (gt)
AH là đường trung tuyến của ∆ABC (cmt)
⇒ AH = HB = HC = BC : 2
Tứ giác AHBK có:
D là trung điểm HK (cmt)
D là trung điểm AB (cmt)
⇒ AHBK là hình bình hành
Mà AH ⊥ BH (cmt)
⇒ AHBK là hình chữ nhật
Lại có AH = BH (cmt)
⇒ AHBK là hình vuông
Đúng 1
Bình luận (0)
Cho Tam giác ABC cân tại A có AH là đường cao. Gọi M,N lần lượt là trung điểm AB và AC. Gọi K là điểm đối xứng của H qua M a) chứng minh AHBK là hình chữ nhật b) Tứ giác AKHC là hình gì? Vì sao c) Chứng minh AMHN là hình thoi d) tính diện tích Tam giác ABC biết AH=4cm, BC=8cm
a: Xét tứ giác AHBK có
M là trung điểm của AB
M là trung điểm của HK
Do đó: AHBK là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBK là hình chữ nhật
b:
Xét tứ giác AKHC có
AK//HC
AK=HC
Do đó: AKHC là hình bình hành
c: Xét ΔABC có
N là trung điểm của AC
H là trung điểm của BC
Do đó: NH là đường trung bình
=>NH//AB và NH=AB/2
hay NH//AM và NH=AM
=>AMHN là hình bình hành
mà AM=AN
nên AMHN là hình thoi
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại a có đường cao AH(H €BC).Gọi D là trung điểm của đoạn thẳng AB.Gọi K là điểm đối xứng với điểm H qua D
a, Chứng minh tứ giác AHBK là hình chữ nhật
b,Cho AH=9cm,BC=16cm.Tính diện tích tam giác ADH
c,Trên tia đối của tia HA lấy điểm E.Kẻ HF vuông góc với EC(F € EC). Gọi M,N lần lượt là trung điểm của HF, FC.Chứng minh rằng :BF vuông góc với EM
Xem chi tiết
a) Xét tứ giác AHBK có
D là trung điểm của đường chéo AB(gt)
D là trung điểm của đường chéo KH(K đối xứng với H qua D)
Do đó: AHBK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AHBK có \(\widehat{AHB}=90^0\)(AH⊥BC)
nên AHBK là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Xét ΔABC cân tại A có AH là đường cao ứng với cạnh đáy BC(AH⊥BC)
nên H là trung điểm của BC(Định lí tam giác cân)
⇒\(BH=\dfrac{BC}{2}=\dfrac{16}{2}=8cm\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=8^2+9^2=145\)
\(\Leftrightarrow AB=\sqrt{145}\)(cm)
Xét ΔABH vuông tại H có HD là đường trung tuyến ứng với cạnh AB(D là trung điểm của AB)
nên \(HD=\dfrac{AB}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AD=\dfrac{AB}{2}\)(D là trung điểm của AB)
nên \(HD=AD=\dfrac{AB}{2}=\dfrac{\sqrt{145}}{2}cm\)
Nửa chu vi của tam giác ADH là:
\(P_{ADH}=\dfrac{HD+AD+AH}{2}=\dfrac{\left(\dfrac{\sqrt{145}}{2}+\dfrac{\sqrt{145}}{2}+8\right)}{2}=\dfrac{\sqrt{145}+8}{2}cm\)
Diện tích của tam giác ADH là:
\(S_{ADH}=\sqrt{P\cdot\left(P-AD\right)\cdot\left(P-AH\right)\cdot\left(P-DH\right)}\)
\(=\sqrt{\dfrac{\sqrt{145}+8}{2}\cdot\left(\dfrac{\sqrt{145}+8}{2}-\dfrac{\sqrt{145}}{2}\right)\cdot\left(\dfrac{\sqrt{145}+8}{2}-\dfrac{\sqrt{145}}{2}\right)\cdot\left(\dfrac{\sqrt{145}+8}{2}-8\right)}\)
\(=\sqrt{\dfrac{\sqrt{145}+8}{2}\cdot16\cdot\dfrac{\sqrt{145}-8}{2}}\)
\(=\sqrt{\dfrac{145-64}{2}\cdot16}\)
\(=\sqrt{\dfrac{81}{2}\cdot16}=18\sqrt{2}cm^2\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A . Gọi H và D lần lượt là trung điểm của BC và AB
a) Chứng minh DH vuông góc BA
b) Gọi K là điểm đối xứng với E qua D . Chứng minh tứ giác AHBK là hình vuông.
Bài 1:Cho tam giác ABC vuông tại A,đường cao AH.Gọi D là là điểm đối xứng với H qua AB M là giao điểm của AB và DH. Gọi E là đối xứng với H qua AC ,N là giao điểm của AC và HE.a)Chứng minh tứ giác AMHN là hình chữ nhật b)Chứng minh rằng D đối xứng với E qua Ac) Tìm điều kiện của tam giác ABC để tứ giác AMHN là hình vuông.Bài 2:Cho tam giác ABC cân tại A,có đường cao AH. Gọi M là trung điểm của AC, K là điểm đối xứng của H qua M.a)Chứng minh tứ giác AMHN là hình chữ nhật.b)Tứ giác ABHK là hình gì...
Đọc tiếp
Bài 1:
Cho tam giác ABC vuông tại A,đường cao AH.Gọi D là là điểm đối xứng với H qua AB M là giao điểm của AB và DH. Gọi E là đối xứng với H qua AC ,N là giao điểm của AC và HE.
a)Chứng minh tứ giác AMHN là hình chữ nhật
b)Chứng minh rằng D đối xứng với E qua A
c) Tìm điều kiện của tam giác ABC để tứ giác AMHN là hình vuông.
Bài 2:
Cho tam giác ABC cân tại A,có đường cao AH. Gọi M là trung điểm của AC, K là điểm đối xứng của H qua M.
a)Chứng minh tứ giác AMHN là hình chữ nhật.
b)Tứ giác ABHK là hình gì?Chứng minh.
c)Tìm điều kiện của tam giác ABC để là hình vuông.
Cho tam giác ABC vuông cân tại A, đường cao AH (H BC ). Có M và N lần
lượt là hình chiếu của H trên AB và AC.
a) Tứ giác AMHN là hình gì?
b) Gọi E là điểm đối xứng với B qua A; F là điểm đối xứng với C qua A. Tứ giác BCEF là hình
gì? Vì sao?
c) Đường thẳng BN cắt CE tại K.Chứng minh
ck=1/3bc
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{NAM}=90^0\)
Do đó: AMHN là hình chữ nhật
mà AM=AN
nên AMHN là hình vuông
b: Xét tứ giác CEFB có
A là trung điểm của CF
A là trung điểm của EB
Do đó CEFB là hình bình hành
mà CF=EB
nên CEFB là hình chữ nhật
mà CF⊥EB
nên CEFB là hình vuông
Đúng 2
Bình luận (0)
cho tam giác abc cân tại a,đường cao ah.gọi ilaf trung điểm ab,k là điểm đối xứng của h qua i.a) tứ giác ahbk là hình j vì sao
b)ACHI là hình j vì sao
c)nếu tam giác ABC đều thì ACHI là hình j vì sao
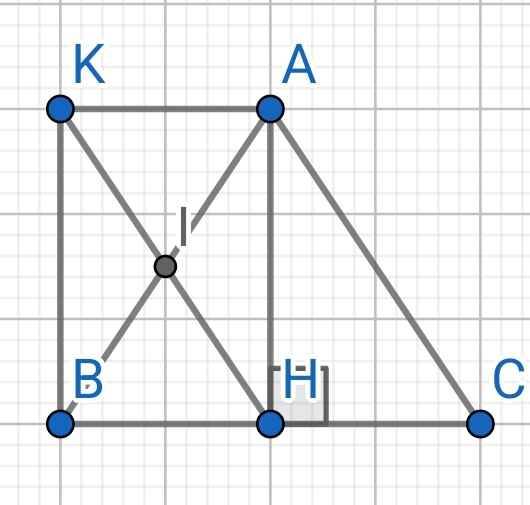 a) Do H và K đối xứng nhau qua I
a) Do H và K đối xứng nhau qua I
⇒ I là trung điểm của HK
Do AH là đường cao của ∆ABC
⇒ AH ⊥ BC
⇒ ∠AHB = 90⁰
Tứ giác AHBK có:
I là trung điểm HK (cmt)
I là trung điểm AB (gt)
⇒ AHBK là hình bình hành
Mà ∠AHB = 90⁰ (cmt)
⇒ AHBK là hình chữ nhật
b) ∆ABC cân tại A (gt)
AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm BC
Mà I là trung điểm AB (gt)
⇒ HI là đường trung bình của ∆ABC
⇒ HI // AC
Tứ giác ACHI có:
HI // AC (cmt)
⇒ ACHI là hình thang
c) ∆ABC đều
⇒ ∠BAC = ∠ACB = 60⁰
⇒ ∠IAC = ∠ACH = 60⁰
Mà ACHI là hình thang (cmt)
⇒ ACHI là hình thang cân
Đúng 1
Bình luận (0)
Cho \(\Delta\)ABC cân tại A có đường cao AH , I là trung điểm AB , K đối xứng H qua I
a) Biết AB = 6cm. Tính IH
b) CM: AHBK là HCN
c) Tam giác ABC có thêm điều kiện gì thì HCN AHBK là Hình vuông
a) Do \(\Delta ABH\)vuông (gt):
mà I Trung điểm AB (gt)
nên \(HI=\frac{1}{2}AB=\frac{6}{2}=3cm\)
b) Xét Tứ giác AHBK:
HI = HK (gt)
AI = AB (gt)
=> Tứ giác ABHK là hình bình hành (2 đường chéo cắt nhau tai trung điểm mỗi đường)
mà \(HI=\frac{1}{2}AB\Leftrightarrow2HI=AB\Leftrightarrow HK=AB\)
=> Hình bình hành ABHK là hình chữ nhật (đpcm).
c) Điều kiện để HCN ABHK là hình vuông thì \(\Delta ABC\)thì:
Dường cao AH = HB
=> HCN AHBK là hình vuông.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có AH là đường cao. Gọi M, N là trung điểm 2 cạnh AB, AC. Biết AH16 cm, BC12 cm a) tính DT tam giác AC, đội dài MNb) Gọi E là điểm đối xứng của H qua M. Cm tứ giác AHBE là ình chữ nhậtC) Gọi F là điểm đối xứng của A qua H. Cm tứ giác ABFC là hình thoid) Gọi K là hình chiếu ủa H lên cạnh FC, gọi I là trung điểm HK. Cm BK vuông góc IFGIÚP MÌNH CÂU d) VỚI !!!
Đọc tiếp
Cho tam giác ABC cân tại A có AH là đường cao. Gọi M, N là trung điểm 2 cạnh AB, AC. Biết AH=16 cm, BC=12 cm
a) tính DT tam giác AC, đội dài MN
b) Gọi E là điểm đối xứng của H qua M. Cm tứ giác AHBE là ình chữ nhật
C) Gọi F là điểm đối xứng của A qua H. Cm tứ giác ABFC là hình thoi
d) Gọi K là hình chiếu ủa H lên cạnh FC, gọi I là trung điểm HK. Cm BK vuông góc IF
GIÚP MÌNH CÂU d) VỚI !!!
4) Gọi D là trung điểm của CK.
ΔABC cân ở A có AH là đường cao, đồng thời là đường trung tuyến
⇒ CH ⊥ FH; H là trung điểm của BC
⇒ DH là đường trung bình của ΔBCK ⇒ DH // BK.
I là trung điểm của HK ⇒ DI là đường trung bình của ΔCHK
⇒ DI // CH ⇒ DI ⊥ FH.
K là hình chiếu của H lên CF ⇒ HI ⊥ DF
⇒ I là trực tâm của ΔDFH ⇒ FI ⊥ DH ⇒ FI ⊥ BK.
Đúng 0
Bình luận (0)
a) diện tích của tam giác ABC là SABC=1/2.AH.BC=1/2.16.12=96 tam giác ABC có M là trung điểm AB N là trung điểm AC nên MN là đường trung bình của tam giác ABC => MN=1/2BC=1/2.12=6 vậy MN=6
Đúng 0
Bình luận (0)


















