Cho hình chóp SABCD có đáy là hình thang (AB//CD). Gọi M là trung điểm của SD.
a. Xác định giao điểm của SD và MA.
b. Gọi M là trung điểm của SC.
Chứng minh: MN//CD
Đề bài sai òi :v Vẽ hình ra đi bạn.
Giờ tui gán MN vô (SBD) thì giao tuyến của (SBD) và (SBC) là SB. Vậy nên SB phải song song với MN. Nhưng ko :) Song song chết liền hà :)
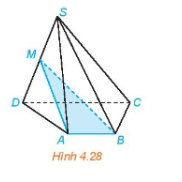
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28)
a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD).
b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.
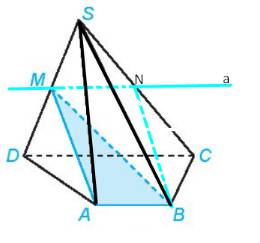
a) mp(MAB) và (SCD)có điểm M chung và chứa hai đường thẳng thẳng song song là AB và CD
Do đó giao tuyến của hai mặt phẳng (MAB) và (SCD) là đường thẳng a đi qua M và song song với CD, AB.
b, Do MN //CD và M là trung điểm của SD.
Suy ra, MN là đường trung bình của tam giác SCD.
Help me !!! cần gấp ạ .mn giúp mình câu c
a) Do MN\(\subset\) (BMN); AD \(\subset\)(ABCD) nên I là một điểm chung của (BMN) với (ABCD). Dễ thấy B là một điểm chung khác I
Vậy (BMN)\(\cap\) (ABCD) =BI
b) J\(\in\)BI\(\subset\) (BMN)
J \(\in\) (CD) \(\subset\) (SCD)
nên J là một điểm chung của (BMN) \(\cap\) (SCD)
vậy (SCD) \(\cap\) (BMN) =NJ
Thiết diện của (BMN) với hình chóp là tứ giác AMNJ
c) Áp dụng định lí Menelaus Trong \(\Delta SAD\) có cát tuyến MNI có:
\(\dfrac{ID}{IA}.\dfrac{MA}{MS}.\dfrac{NS}{ND}=1\)
\(\dfrac{ID}{IA}.1.2=1\) => \(\dfrac{ID}{IA}=\dfrac{1}{2}\)
=> D là trung điểm AI
+ Xét tam giác SAI có 2 trung tuyến MI, SD giao nhau tại N => N là trong tâm tam giác SAI
=> \(\dfrac{NI}{MI}=\dfrac{2}{3}\)
Ta có AD//BC
=> \(\dfrac{IK}{BK}=\dfrac{AI}{BC}=\dfrac{2AD}{BC}=2\)(do AD=BC)
=> \(\dfrac{IK}{IB}=\dfrac{2}{3}\)
Xét tam giác MIB có: \(\dfrac{NI}{MI}=\dfrac{IK}{IB}=\dfrac{2}{3}\)
=> BM//NK
Cho hình chóp S.ABCD có đáy là hình bình hành, tâm O. Gọi M, N lần lượt là trung điểm của AB, CD.
1. Xác định giao tuyến của (SBC) và (SAD).
2. Chứng minh MN // (SBC); MN // (SAD).
3. Gọi I là trung điểm của SA. Tìm giao điểm K của (INM) và SD.
4. Chứng minh SB, SC // (IMN).
5. Gọi H là trung điểm của IO. Chứng minh HK // (SBC).
giải giúp mình với
Cho hình chóp SABCD có đáy ABCD là hình bình hành, M là trung điểm SA. điểm N thuộc đoạn SD sao cho NS=2ND, I là giao điểm của MN với AD.
a) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABCD).
b) Gọi J là giao điểm của CD với BI .Xác dinh giao tuyến của mặt phẳng (BMN) với (SCD), từ đó suy ra thiết diện của hình chóp với mặt phẳng (BMM).
c) Gọi K là giao điểm của BI với AC. Chứng minh BM // KN
Trong tam giác SBD, MN là đường trung bình \(\Rightarrow MN||BD\)
\(\Rightarrow MN||\left(ABCD\right)\)
Trong mp (ABCD), qua E kẻ đường thẳng song song BD cắt BC tại F và cắt AD kéo dài tại G
Trong mp (SAD), nối GN kéo dài cắt SA tại P
Ngũ giác PNEFM là thiết diện của (MNE) và chóp
Cho hình chóp SABCD có đáy ABCD là hình thang, đáy lớn là AD. Gọi M,N,P lần lượt là trung điểm của AB,SA,SD.
a. Tìm giao tuyến của 2 mp (SAB) và (SCD)
b. chứng minh NP // (SBC)
c. tìm giao điểm của SC với mp(MNP)
Cho hình chóp SABCD có đáy ABCD là hình thang với AB//CD. Gọi M,N,P,Q lần lượt là trung điểm của SD,SC,SB,SA. Chứng minh (MNPQ)//(ABCD)
Do M là trung điểm SD, N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow MN||CD\) (1)
Tương tự PQ là đường trung bình tam giác SAB \(\Rightarrow PQ||AB\)
\(\Rightarrow MN||PQ\Rightarrow\) 4 điểm M, N, P, Q đồng phẳng
Lại có MQ là đường trung bình tam giác SAD \(\Rightarrow MQ||AD\)
Mà \(AD\in\left(ABCD\right)\Rightarrow MQ||\left(ABCD\right)\)
Do \(CD\in\left(ABCD\right)\), từ \(\left(1\right)\Rightarrow MN||\left(ABCD\right)\)
Mà \(\left\{{}\begin{matrix}MN\in\left(MNPQ\right)\\MQ\in\left(MNPQ\right)\\MN\cap MQ=M\end{matrix}\right.\)\(\Rightarrow\left(MNPQ\right)||\left(ABCD\right)\)
Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn AB, M là trung điểm của SD.
a. Tìm giao tuyến của (ABM) và (SCD).
b. Gọi N là trung điểm của SC, P là một điểm trên cạnh BC và khác với điểm B và điểm C. Tìm giao điểm Q của SD với (ANP).