Chứng minh rằng
(m+1)2>= 4m
m2+n2+2>=2(m+n)
Những câu hỏi liên quan
Chứng minh rằng : m2+n2+2 > 2 (m+n)
Ta có:
m2-2m+1+n2-2n+1
=(m-1)2+(n-1)2>0
Đpcm
Đúng 0
Bình luận (0)
Dễ thui Ta có: 2 = 2 mà đây là tổng
=> đẳng thức trên lớn hơn 2
Bừa hìhif
Đúng 0
Bình luận (0)
FRT_I Love Class 6A ngu thì đừng làm bừa cho người khác hiểu nhầm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
“Chứng minh rằng
2
là số vô tỉ”. Một học sinh đã làm như sau: Bước 1: Giả sử
2
là số hữu tỉ, tức là
2
m
n
, trong đó m, n ∈ N* , (m, n) 1 Bước 2: Từ
2
m
n
m2 2n2 m2 là số chẵn m là số chẵn m 2k, k ∈ N*. n2 2k2 n2 là số chẵn n là số chẵn Bước 3: Do đó...
Đọc tiếp
“Chứng minh rằng 2 là số vô tỉ”. Một học sinh đã làm như sau:
Bước 1: Giả sử 2 là số hữu tỉ, tức là 2 = m n , trong đó m, n ∈ N* , (m, n) = 1
Bước 2: Từ 2 = m n => m2 = 2n2 => m2 là số chẵn
=> m là số chẵn => m = 2k, k ∈ N*.
=> n2 = 2k2 => n2 là số chẵn => n là số chẵn
Bước 3: Do đó m chẵn, n chẵn mâu thuẫn với (m, n) = 1.
Bước 4: Vậy 2 là số vô tỉ.
Lập luận trên đúng tới bước nào?
A. Bước 1.
B. Bước 2.
C. Bước 3.
D. Bước 4.
Đáp án: D
Các bước giải bài toán trên đều đúng.
Đúng 0
Bình luận (0)
Bài 2.Cho m,n là hai số nguyên dương sao cho m2022+ m + n2 chia hết cho mn. Chứng minh rằng m là số chính phương.
Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m2 + n2 = 2(a2 + b2).
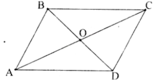
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
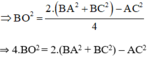
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
Đúng 0
Bình luận (0)
Với số m và số n bất kì, chứng tỏ rằng: m 2 + n 2 + 2 ≥ 2(m + n)
Ta có: m - 1 2 ≥ 0; n - 1 2 ≥ 0
⇒ m - 1 2 + n - 1 2 ≥ 0
⇔ m 2 – 2m + 1 + n 2 – 2n + 1 ≥ 0
⇔ m 2 + n 2 + 2 ≥ 2(m + n)
Đúng 0
Bình luận (0)
18 tháng 7 2021 lúc 16:13
1.Chứng minh rằng \(2^{2^{6n+2}}+3⋮19\) với ,mọi n\(\in\)N
2.Chứng minh rằng với n>0 ta có 52n-1.22n-15n+1+3n+1.22n-1 chia hết cho 38
Chứng minh rằng với mọi số nguyên n thì (2 - n) ( n2 - 3n + 1) + n (n2 + 12 )+ 8 chia hết cho 5
\(\left(2-n\right)\left(n^2-3n+1\right)+n\left(n^2+12\right)+8\)
\(=2n^2-6n+2-n^3+3n^2-n+n^3+12n+8\)
\(=5n^2+5n+10\)
\(=5\left(n^2+n+2\right)⋮5\) (đpcm)
Đúng 4
Bình luận (0)
Chứng minh rằng: A = n 2 + n + 1 không chia hết cho 2, với ∀ n ∈ N
Chứng minh rằng: A=n2+n+1 ko chia hết cho 2 và 5,∀ n∈N
n 2+n+1 = n(n + 1) +1.
Vì n(n+1) là tích của hai số tự nhiên liên tiếp nên có chữ số tận cùng là 0, 2, 6
Do đó n(n+1) + 1 có chữ số tận cùng là 1, 3, 7.
Vì 1, 3, 7 không chia hết cho 2 và 5 nên n(n+1) + 1 không chia hết cho 2 và 5
Vậy n 2+n+1 không chia hết cho 2 và 5
Đúng 4
Bình luận (0)
a) n2+n+1=n(n+1)+1
Ta có n(n+1)⋮2vì n(n+1)n(n+1)là tích 2 số TN liên tiếp . Do đó n(n+1)+1không chia hết cho 2
- n2+n+1=n(n+1)+1
Ta có n(n+1)l là tích của 2 số TN liên tiếp nên tận cùng bằng 0,2,6 . Suy ra n(n+1)tận cùng bằng 1,3,7 không chia hết cho 5
Đúng 1
Bình luận (0)
tham khao
https://olm.vn/hoi-dap/detail/93364253.html
Đúng 0
Bình luận (0)
30 tháng 10 2021 lúc 19:28
Chứng minh rằng:
(n - 1)2 (n + 1) + (n2 - 1)
luôn chia hết cho 6 với mọi số nguyên n
\(\left(n-1\right)^2\cdot\left(n+1\right)+\left(n^2-1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)
\(=\left(n-1\right)\cdot n\cdot\left(n+1\right)⋮6\)
Đúng 1
Bình luận (0)