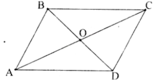
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
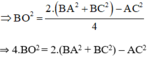
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).

Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
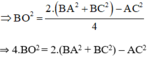
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
Cho hình bình hành ABCD có AB=a, BC=b, DB=m và AC=n. Chứng minh rằng \(^2m+n^2=2\left(a^2+b^2\right)\)
a) Cho tứ giác ABCD không phải là hình bình hành, AC cắt BD tại O có OB = OD. Gọi M, N lần lượt là trung điểm của AB và CD, MN cắt AC tại I. Chứng minh rằng \(\overrightarrow{MI}=\overrightarrow{IN}\)
b) Cho tứ giác ABCD có 2 đường chéo cắt nhau tại I. Biết \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\). Chứng minh rằng tứ giác ABCD là hình bình hành
1)Cho hình bình hành ABCD, xác định các vectơ DA+DC,AB+DA.
2)Cho 5 điểm A, B, C, D, E. Chứng minh rằng: AC-ED+CD+EC-BC = AB
3)Cho hình vuông ABCD, tâm O cạnh bằng a.
a) Xác định vecto BA+DA+AC, AB+CA+BC, AB+AC.
b) Tính độ dài vecto DA+DC, AB-BC
Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C. BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
1) Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một đường tròn.
cho hình bình hành ABCD tâm O, M là trung điểm OB
a, chứng minh vecto AB- vecto DA +vecto CD=vecto AD
b, điểm N thuộc BC thỏa mãn vecto BN=k vectoBC , tìm k để A,M,N thẳng hàng
Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C.BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
2) CM cắt QN tại K, CN cắt PM tại L. Chứng minh rằng K L ⊥ O C .
Cho hình bình hành ABCD. Biết rằng \(\overrightarrow{BD}\) = m\(\overrightarrow{BA}\) +n\(\overrightarrow{BC}\) với m, n là các số thực. Tính giá trị của S = 20m +21n.
Cho a, b, c là độ dài ba cạnh của một tam giác.
a) Chứng minh (b - c)2 < a2
b) Từ đó suy ra: a2 + b2 + c2 < 2(ab + bc + ca)
cho hình chữ nhật abcd có cạnh ab = 8, bc = 6 lấy điểm m bất kì , chứng minh rằng vectơ ac + bm = am + bc