Cho đường thẳng (d1): y=-x-1; (d2): y= x-5.
a) Tìm tọa độ giao điểm A của (d1) và (d2)
b) c/m(d1) vuông góc với (d2), Tính chu vi tam giác tạo bởi (d1), (d2) và trục Oy
Câu 3:Cho đường thẳng (d1):y=(m-1)x+4.Tìm giá trị của m để:
a)Đường thẳng (d1) và đường thẳng (d2):y=(2m+3)x+3m-1 song song với nhau.
b)Đường thẳng (d1) và đường thẳng (d3):y=x+2m+2 cắt nhau tại một điểm có tung độ bằng 3.
c)Đường thẳng (d1) tiếp xúc với đường tròn tâm O bán kính 2\(\sqrt{2}\)(với O là gốc tọa độ)
Để hàm số y=(m-1)x+4 là hàm số bậc nhất thì \(m-1\ne0\)
hay \(m\ne1\)
a) Để (d1) và (d2) song song với nhau thì \(\left\{{}\begin{matrix}m-1=2m+3\\3m-1\ne4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-2m=3+1\\3m\ne5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-m=4\\3m\ne5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-4\\m\ne\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow m=-4\)
Kết hợp ĐKXĐ, ta được: m=-4
Vậy: Để (d1) và (d2) song song với nhau thì m=-4
Cho hàm số bậc nhất y=2mx + m - 1 có đồ thị (d1). Tìm m để:
a) Đường thẳng (d1) song song với đường thẳng y= -\(\dfrac{1}{3}\)x + 1
b) (d1) trùng với đường thẳng -2x - y = 5
a.
Để hai đường thẳng song song:
\(\Rightarrow\left\{{}\begin{matrix}2m=-\dfrac{1}{3}\\m-1\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{1}{6}\\m\ne2\end{matrix}\right.\) \(\Leftrightarrow m=-\dfrac{1}{6}\)
b.
\(-2x-y=5\Leftrightarrow y=-2x-5\)
Để hai đường thẳng trùng nhau:
\(\Leftrightarrow\left\{{}\begin{matrix}2m=-2\\m-1=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m=-4\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
Vậy ko tồn tại m để 2 đường thẳng trùng nhau
Cho điểm A(1; 1) và hai đường thẳng ( d 1 ): y = x − 1; ( d 2 ): y = 4x − 2. Viết phương trình đường thẳng (d) đi qua điểm A và cắt các đường thẳng (d1), ( d 1 ) tạo thành một tam giác vuông.
A. y = 2x–1
B. y = –2x+3
C. y = − x + 2 y = − 1 4 x + 5 4
D. Không xác định được
Bài II (3,0 điểm) Cho 2 đường thẳng: (d1): y= +2x 4 và (d2): y=− +x 1 .
1) Tìm tọa độ giao điểm A của đường thẳng (d1) và đường thẳng (d2).
2) Xác định hệ số a, b của đường thẳng y ax b= + (a0) biết đường thẳng đó song song với đường thẳng (d1) và đi qua điểm M (-1; 3).
3) Gọi B và C lần lượt là giao điểm của đường thẳng (d1) và (d2) với trục hoành. Tính diện tích tam giác ABC.
1, PT hoành độ giao điểm: \(2x+4=-x+1\Leftrightarrow x=-1\Leftrightarrow y=0\)
\(\Leftrightarrow A\left(-1;0\right)\)
Vậy \(A\left(-1;0\right)\) là tọa độ giao điểm 2 đths
2, Đt cần tìm //(d1)\(\Leftrightarrow a=2;b\ne4\)
Đt cần tìm đi qua M(-1;3) nên \(-a+b=3\Leftrightarrow-2+b=3\Leftrightarrow b=5\left(tm\right)\)
Vậy đths là \(y=2x+5\)
3, PT giao điểm d1 với trục hoành là \(y=0\Leftrightarrow2x+4=0\Leftrightarrow x=-2\Leftrightarrow B\left(-2;0\right)\)
PT giao điểm d2 với trục hoành là \(y=0\Leftrightarrow-x+1=0\Leftrightarrow x=1\Leftrightarrow C\left(1;0\right)\)
Do đó \(BC=\left|-2\right|+\left|1\right|=3;OA=\left|-1\right|=1\)
Vậy \(S_{ABC}=\dfrac{1}{2}OA\cdot BC=\dfrac{3}{2}\left(đvdt\right)\)
Cho hàm số bậc nhất y= (m+1)x +m -1 (m là tham số) có đồ thị là (d1). Tìm m để:
a) Hàm số đồng biến
b) Đường thẳng (d1) đi qua điểm A(1;2)
c) Đường thẳng (d1) song song với đường thẳng y=-\(\dfrac{1}{3}\)x + 1
a) Hàm số đồng biến `<=>m+1>0<=>m>-1`
b) `d_1` đi qua `A(1;2) <=> 2=(m+1).1+m-1<=>m=1`
c) `d_1 //// y=-1/3 x+1 <=>` \(\left\{{}\begin{matrix}m+1=-\dfrac{1}{3}\\m-1\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{4}{3}\\m\ne2\end{matrix}\right.\Leftrightarrow m=-\dfrac{4}{3}\)
Bài 1: cho 2 đường thẳng y=(m-3)x+3 (d1) và y= -x+m (d2). Tìm m để (d1)// (d2)
Bài 2: cho 2 đường thẳng y=2x (d1) và y= -x+3 (d2)
a) tìm tọa độ giao điểm A của (d1) và (d2)
b) viết phương trình đường thẳng (d3) qua A và // với đường thẳng y= x+4 (d)
Giải chi tiết dùm mình với ạ :<
BÀI 1
để d1 và d2 // thì: m-3=-1(1) ; m khác 3 (2)
ta có: (1) <=> m=2 (3)
từ (2) và (3) => để d1//d2 thì m = 2
Cho hai đường thẳng d1 : x+ y -1= 0 và d2 : x- 3y + 3= 0. Phương trình đường thẳng d đối xứng với d1 qua đường thẳng d2 là:
A.x-7y +1 =0
B.x+7y +1= 0
C. 7x+y+1= 0
D. 7x-y+1= 0
Đáp án D
+Giao điểm của d1 và d2 là nghiệm của hệ
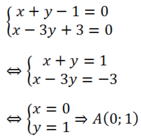
+Lấy M(1 ; 0) thuộc d1. Tìm M’ đối xứng M qua d2
+Viết phương trình đường thẳng ∆ đi qua M và vuông góc với d2 là
3(x-1) + 1( y=0) =0 hay 3x+ y-3= 0
Gọi H là giao điểm của ∆ và đường thẳng d2. Tọa độ H là nghiệm của hệ
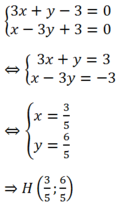
Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ:
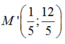
Viết phương trình đường thẳng d đi qua 2 điểm A và M’ : đi qua A(0 ;1) , vectơ chỉ phương 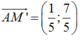
=> vectơ pháp tuyến 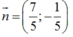
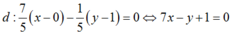
cho hai đường thẳng d1:y=-x+2 và d2:y=-x/3-1/2
a) vẽ trên cùng một mặt phẳng Oxy hai đường thẳng d1; d2
b) viết pt đường thẳng đi qua điểm N ∈ d2 có hoành độ Xn = 3/4 đồng thời song song với đường thẳng d1
b: \(y_N=-\dfrac{3}{4}:3-\dfrac{1}{2}=\dfrac{-1}{4}-\dfrac{1}{2}=-\dfrac{3}{8}\)
Vì (d)//(d1) nên a=-1
Vậy: (d): y=-x+b
Thay x=3/4 và y=-3/8 vào (d), ta được:
b-3/4=-3/8
hay b=3/8
Cho hai đường thẳng y = ax +b (d1) và y= x+ 2 (d2)
Tìm a, b biết đường thẳng (d1) song song với đường thẳng (d2) và qua A(-1; 2)
Lời giải:
Vì $(d_1)\parallel (d_2)$ nên $a=1$
$A\in (d_1)$ nên $y_A=ax_A+b\Leftrightarrow 2=a(-1)+b$
$\Leftrightarrow b=2+a=2+1=3$
Vậy $a=1; b=3$
trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d1): y=2x+4 (d2): y=-x+4, (dm): y= (m+3)x-7(m≠3)
1) Xác định giá trị m để đường thẳng (dm) // với đường thẳng (d1)
2) Xác định giá trị của m để đường thẳng (d1) và đường thẳng (d2) trên cùng mặt phẳng tọa độ Oxy
3)Gọi A và B lần lượt là giao điểm của đường thẳng (d1) và đường thẳng (d2) với trục Ox. Tìm tọa độ các điểm A và B
5) Tính diện tích tam giác ABC (đơn vị các trục tọa độ cm)
1: Để hai đường song song thì m+3=2
hay m=-1
3: Tọa độ của điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\2x+4=0\end{matrix}\right.\Leftrightarrow A\left(-2;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}y_B=0\\-x+4=0\end{matrix}\right.\Leftrightarrow B\left(4;0\right)\)