CMR
a) (-x)2n=x2n b) (-x)2n+1=-x2n+1
Những câu hỏi liên quan
cho
f(x)= x2n-x2n-1+....+x2-x+1 (xϵN)
g(x)=-x2n+1+x2n-x2n-1+....+x2-x=1
tính giá trị của hiệu f(x)-g(x) tại x=\(\dfrac{1}{10}\)
Biểu thức D
x
(
x
2
n
-
1
+
y
)
–
y
(
x
+
y
2
n
-
1
)
+
y
2
n...
Đọc tiếp
Biểu thức D = x ( x 2 n - 1 + y ) – y ( x + y 2 n - 1 ) + y 2 n – x 2 n + 5 , D có giá trị là:
A. 2 y 2 n
B. -5
C. x 2 n
D. 5
Ta có
D = x ( x 2 n - 1 + y ) – y ( x + y 2 n - 1 ) + y 2 n – x 2 n + 5
= x . x 2 n - 1 + x . y – y . x – y . y 2 n - 1 + y 2 n – x 2 n + 5
= x 2 n + x y – x y – y 2 n + y 2 n – x 2 n + 5
= ( x 2 n – x 2 n ) + ( x y – x y ) + ( y 2 n – y 2 n ) + 5
= 0 + 0 + 0 + 5 = 5
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Chứng minh rằng :
a) 1x3x5x....x39/21x22x23x....x40 = 1/2 mũ 20
b) 1x3x5x....x(2n-1)/(n+1)x(n+2)x....x2n = 1/2 mũ n (n e N* )
mk cần gấp lắm 
a) Nhân cả tử và mẫu với 2.4.6...40 ta được :
\(\frac{1.3.5...39}{21.22.23...40}\)=\(\frac{\left(1.3.5...39\right)\left(2.4.6..40\right)}{\left(21.22.23...40\right)\left(2.4.6...40\right)}\)
= \(\frac{1.2.3...39.40}{21.22.23...40.\left(1.2.3...20\right).2^{20}}\)
=\(\frac{1}{2^{20}}\)
b) Nhân cả tử và mẫu với 2.4.6...2n rồi biến đổi như câu a.
Đúng 2
Bình luận (4)
Tìm số tự nhiên n để X ⋮ Y biết X= 7 x2n -1-5x3;Y=5xn.
\(\dfrac{X}{Y}=\dfrac{7}{5}x^{n-1}-x^{3-n}\)
Để X chia hết cho Y thì n-1>=0 và 3-n>=0
=>1<=n<=3
=>\(n\in\left\{1;2;3\right\}\)
Đúng 0
Bình luận (0)
Cho đa thức A(x) = 1 + x2 + x4 + .... + x2n - 2; B= 1 + x + x2 + ... + xn-1. Tìm số nguyên dương n để đa thức A(x) chia hết cho đa thức B(x).
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
Đúng 1
Bình luận (1)
Tìm số tự nhiên n để đa thức:
A(x)=x2n+xn+1 chia hết cho đa thức x2+x+1.
Vì \(A\left(x\right)=x^{2n}+x^n+1\) chỉ có một hằng số là1
đa thức \(x^2+x+1\) cũng chỉ có một hằng số là 1
Để \(A\left(x\right)⋮x^2+x+1\) thì thì \(A\left(x\right)\) phải có số mũ tương ứng với các bậc như đa thức : => n=1
Đúng 1
Bình luận (0)
-Đáp án cuối cùng: \(n=3k+1\) hay \(n=3k+2\)
Tìm số tự nhiên n để đa thức:
A(x)=x2n+xn+1 chia hết cho đa thức x2+x+1.
Giả sử
1
-
x
+
x
2
n
a
0
+
a
1
x
+
a
2
x
2
+
....
Đọc tiếp
Giả sử 1 - x + x 2 n = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n . Đặt s = a 0 + a 2 + a 4 + . . . + a 2 n , khi đó, s bằng
A. 3 n + 1 2
B. 3 n - 1 2
C. 3 n 2
D. 2 n + 1
Giả sử
1
-
x
+
x
2
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
2...
Đọc tiếp
Giả sử 1 - x + x 2 n = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n . Đặt S = a 0 + a 2 + a 4 + . . . + a 2 n , khi đó S bằng
A. 3 n + 1 2
B. 3 n 2
C. 3 n - 1 2
D. 2 n + 1
Giả sử
1
-
x
+
x
2
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
2...
Đọc tiếp
Giả sử 1 - x + x 2 n = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n . Đặt S = a 0 + a 2 + a 4 + . + a 2 n , khi đó S bằng:
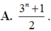
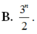
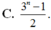
