Cho tam giác ABC vuông tại A biết AB = 3cm, AC = 4 cm tính BC, góc B, góc C

Những câu hỏi liên quan
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A, trung tuyến CM. Qua M kẻ đường thẳng vuông góc với AB cắt BC tại N a) C/m tam giác BAN cân b) Tính BC biết AB=3cm, AC=4cm
a) Xét ΔNAM vuông tại M và ΔNBM vuông tại M có
NM chung
MA=MB(M là trung điểm của AB)
Do đó: ΔNAM=ΔNBM(hai cạnh góc vuông)
Suy ra: NA=NB(Hai cạnh tương ứng)
Đúng 1
Bình luận (1)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Vậy: BC=5cm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH, biết AB = 3cm; AC = 4 cm tính: a) BC,AH,HB b) số đo góc B
a) Áp dụng định lí Py - ta - go vào tam giác vuông ABC ta có:
BC = \(\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}\)
BC = 5 cm
Từ hệ thức của cạnh góc vuông và hình chiếu của nó trên cạnh huyền suy ra:
HB = \(\dfrac{AB^2}{BC}=\dfrac{3^2}{5}=1,8\) cm
Ta có: HB + HC = BC
1,8 + HC = 5
HC = 3,2 cm
Theo hệ thức liên quan đến đường cao ta có:
AH2 = HB . HC
AH2 = 1,8 . 3,2
AH2 = 5,76
⇒ AH = 2,4 cm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Tìm các tỉ số lượng giác của góc B khi : a) BC=5 cm, AB= 3cm. b) BC=13cm, AC= 12cm . c)AC=4 cm, AB= 3cm.
Bài 1: Cho tam giác ABC nhọn, kẻ AH vuông góc BC.
a) Biết B = 50 độ, C = 40 độ. Tính góc BAH và góc HAC.
b) Biết BH = 3cm, HC = AH = 4cm. Tính AB và AC.
Bài 2: Cho tam giác ABC cân tại A và AH vuông góc BC, BK vuông góc AC, AH cắt BK tại M. Nối MC
a) CM: tam giác MBC cân
b) Vẽ tia Bx//MC cắt AH kéo dài tại N. CM: HM=HN
c) CM: tam giác ABN vuông
Xét tam giác BAH
Có B+BAH=900(vì tam giác BAH vuông tại H)
500+BAH=900
=>BAH=900-500
=>BAH=400
Xét tam giác HAC
Có C+HAC=900(Tam giác HAC vuông tại H)
400+HAC= 900
HAC=900-400
HAC=500
B)Xét tam giác ABH
Có AB2 = HB2+AH2(Theo định lý Pi-ta-go)
AB2=32+42
AB2=25=52
AB=5
Xét tam giác CAH
Có AC2=AH2+HC2 (Theo định lý Pi-ta-go)
AC2=42+42=32=
Cho tam giác abc cân tại b . Kẻ bh vuông góc ac (h thuộc ac) Cm a) tam giác abc = tam giác cbh b) cho bh = 4 cm, ac = 6 cm . Tính bc =? c) kẻ he vuông góc ab, hf vuông góc bc . Cm be= bf
Cho tam giác ABC vuông tại A.Đường cao AH vuông góc với BC tại H.AB=3cm ,AC=4 cm a,Chứng minh AB²=HB.HC,AC²=HC.BC b,tính AH c,Kẻ tia phân giác AD của BAC.Tính BD
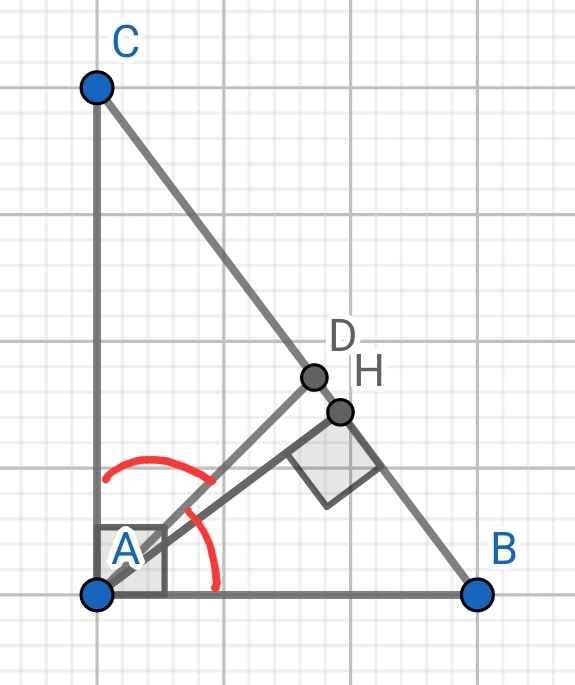
a) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠B = ∠CAH (cùng phụ C)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/HC = HB/AH
⇒ AH.AH = HB.HC
⇒ AH² = HB.HC
Xét hai tam giác vuông: ∆ABC và ∆HAC có:
∠C chung
⇒ ∆ABC ∽ ∆HAC (g-g)
⇒ AC/HC = BC/AC
⇒ AC.AC = HC.BC
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 3² + 4²
= 25
⇒ BC = 5 (cm)
Do AD là tia phân giác của ∠BAC
⇒ BD/CD = AB/AC
⇒ AB/BD = AC/CD
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AB/BD = AC/CD = (AB + AC)/(BD + CD) = (3 + 4)/5 = 7/5
Do AB/BD = 7/5
⇒ BD = AB.5/7 = 3.5/7 = 15/7 (cm)
Đúng 1
Bình luận (0)
cho tam giác ABc vuông tại A Biết AB=3cm, AC=4 cm
a Tính BC
b gọi M là trung điểm của BC. kẻ BH vuông góc AM ại H, CK vuông với AM tịa K. CM tam giác BHM = tam giác CKM
c kẻ HI vuông góc Bc tại H, so sánh HI và MK
d) so sánh BH+BK với BC
a) Tam giác ABC vuông tại A có \(BC^2=AB^2+AC^2\)
=>BC2=32+42=25
=>BC=5
Vậy BC=5 cm
b) Xét tam giác BHM vuông tại H và tam giác CKM vuông tại K có
MC=MB( vì M là trung điểm của BC)
CMK=BHM( 2 góc đối đỉnh)
=> tam giác BHM= tam giác CKM ( cạnh huyền- góc nhọn)
c) Xét tam giác HMI vuông tại I có HM>HI ( cạnh huyền lớn nhất) (1)
Có tam giác BHM= tam giác CKM ( câu b)
=>HM=MK (2)
Từ (1) và (2) =>MK>HI
d) Có \(\Delta BHM=\Delta CKM\)( theo câu b)
=> BH=KC
Xét tam giác BKC có KC+BK>BC ( bất đẳng thức tam giác) (3)
Thay BH=KC vào (3) ta có BH+BK>BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm; BC = 5cm. a/ Tính AC, AH, HB, HC. b/ Tính các tỉ số lượng giác của góc B và tính góc C. c/ Vẽ HM vuông góc AB tại M; vẽ HN vuông góc AC tại N. Chứng minh: AM. AB = AN. AC.
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)

















