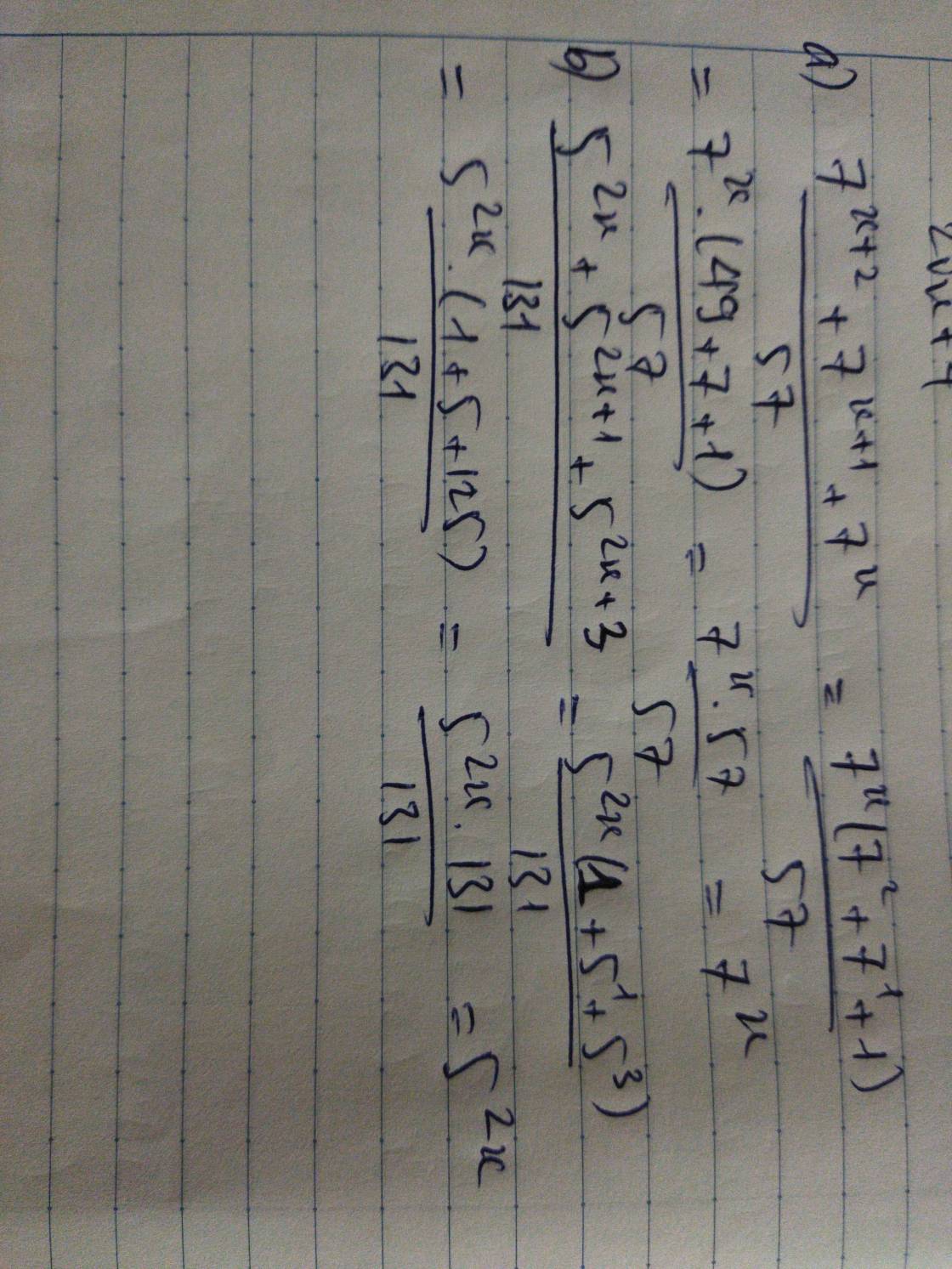\(\frac{2x+3}{2x+1}-\frac{2x+5}{2x+7}=\frac{1-6x^2+9x-9}{\left(2x+1\right)\left(2x+7\right)}\)

\(\Leftrightarrow\frac{\left(2x+3\right)\left(2x+7\right)-\left(2x+5\right)\left(2x-1\right)}{\left(2x+1\right)\left(2x+7\right)}=\frac{1-6x^2+9x-9}{\left(2x+1\right)\left(2x+7\right)}\)

\(\Rightarrow\left(2x+3\right)\left(2x+7\right)-\left(2x+5\right)\left(2x+1\right)=1-6x^2+9x-9\)

\(\Leftrightarrow4x^2+20x+21-4x^2-12x-5=1-6x^2+9x-9\)

\(\Leftrightarrow8x-16=1-6x^2+9x-9\)

\(\Leftrightarrow8x-16-1+6x^2-9x+9=0\)

\(\Leftrightarrow6x^2-x-8=0\)

Tự làm nốt nha 

Trl

-Bạn chuyên toán thcs làm đúng r nhé !~

Học tốt 

nhé bạn ~

\(\frac{2x+3}{2x+1}-\frac{2x+5}{2x+7}=1-\frac{6x^2+9x-9}{\left(2x+1\right)\left(2x+7\right)}\)

\(\Leftrightarrow\frac{\left(2x+3\right)\left(2x+7\right)-\left(2x+5\right)\left(2x+1\right)}{\left(2x+1\right)\left(2x+7\right)}=\frac{\left(2x+7\right)-6x^2-9x+9}{\left(2x+1\right)\left(2x+7\right)}\)

\(\Rightarrow4x^2+20x+21-4x^2-12x-5=2x+7-6x^2-9x+9\)

\(\Leftrightarrow8x+16=-6x^2-7x+16\)

\(\Leftrightarrow6x^2+7x+8x=0\)

\(\Leftrightarrow6x^2+15x=0\)

\(\Leftrightarrow x\left(6x+15\right)=0\)

Đến đây tự làm nốt nha 

hok tốt 

* Trả lời:

\(\left(1\right)\) \(-3\left(1-2x\right)-4\left(1+3x\right)=-5x+5\)

\(\Leftrightarrow-3+6x-4-12x=-5x+5\)

\(\Leftrightarrow6x-12x+5x=3+4+5\)

\(\Leftrightarrow x=12\)

\(\left(2\right)\) \(3\left(2x-5\right)-6\left(1-4x\right)=-3x+7\)

\(\Leftrightarrow6x-15-6+24x=-3x+7\)

\(\Leftrightarrow6x+24x+3x=15+6+7\)

\(\Leftrightarrow33x=28\)

\(\Leftrightarrow x=\dfrac{28}{33}\)

\(\left(3\right)\) \(\left(1-3x\right)-2\left(3x-6\right)=-4x-5\)

\(\Leftrightarrow1-3x-6x+12=-4x-5\)

\(\Leftrightarrow-3x-6x+4x=-1-12-5\)

\(\Leftrightarrow-5x=-18\)

\(\Leftrightarrow x=\dfrac{18}{5}\)

\(\left(4\right)\) \(x\left(4x-3\right)-2x\left(2x-1\right)=5x-7\)

\(\Leftrightarrow4x^2-3x-4x^2+2x=5x-7\)

\(\Leftrightarrow-x-5x=-7\)

\(\Leftrightarrow-6x=-7\)

\(\Leftrightarrow x=\dfrac{7}{6}\)

\(\left(5\right)\) \(3x\left(2x-1\right)-6x\left(x+2\right)=-3x+4\)

\(\Leftrightarrow6x^2-3x-6x^2-12x=-3x+4\)

\(\Leftrightarrow-15x+3x=4\)

\(\Leftrightarrow-12x=4\)

\(\Leftrightarrow x=-\dfrac{1}{3}\)

`a)|2x+1|=5`

`<=>` \(\left[ \begin{array}{l}2x+1=5\\2x+1=-5\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}2x=4\\2x=-6\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}x=2\\x=-3\end{array} \right.\) 

`b)|2x+1|=0`

`<=>2x+1=0`

`<=>2x=-1`

`<=>x=-1/2`

`c)|2x+1|=7`

`<=>` \(\left[ \begin{array}{l}2x+1=7\\2x+1=-7\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}2x=6\\2x=-8\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}x=4\\x=-4\end{array} \right.\) 

`d)|2x+5|=|3x-7|`

`<=>` \(\left[ \begin{array}{l}2x+5=3x-7\\2x+5=7-3x\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}x=12\\5x=2\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}x=12\\x=\dfrac25\end{array} \right.\) 

`e)|2x+7|=1`

`<=>` \(\left[ \begin{array}{l}2x+7=1\\2x+7=-1\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}2x=-6\\2x=-8\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}x=3\\x=-4\end{array} \right.\) 

`g)|x-2|+|2x-3|=2`

Nếu `x>=2=>|x-2|=x-2,|2x-3|=2x-3`

`pt<=>x-2+2x-3=2`

`<=>3x-5=2`

`<=>3x=7`

`<=>x=7/3(tm)`

Nếu `x<=3/2=>|x-2|=2-x,|2x-3|=3-2x`

`pt<=>2-x+3-2x=2`

`<=>5-3x=2`

`<=>3x=3`

`<=>x=1(tm)`

Nếu `3/2<=x<=2=>|x-2|=2-x,|2x-3|=2x-3`

`pt<=>2-x+2x-3=2`

`<=>x-1=2`

`<=>x=3(l)`

`h)|x+2|+|1-x|=3x+2`

Vì `VT>=0=>3x+2>=0=>x>=-2/3`

`=>|x+2|=x+2`

`pt<=>x+2+|1-x|=3x+2`

`<=>|1-x|=2x(x>=0)`

`<=>` \(\left[ \begin{array}{l}2x=1-x\\2x=x-1\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}3x=1\\x=-1\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}x=\dfrac13(TM)\\x=-1(KTM)\end{array} \right.\) 

a.

$|2x+1|=5$
\(\Leftrightarrow \left[\begin{matrix} 2x+1=5\\ 2x+1=-5\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=2\\ x=-3\end{matrix}\right.\)

b.

$|2x+1|=0$

$\Leftrightarrow 2x+1=0$

$\Leftrightarrow x=-\frac{1}{2}$
c.

$|2x+1|=7$

\(\Leftrightarrow \left[\begin{matrix} 2x+1=7\\ 2x+1=-7\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=3\\ x=-4\end{matrix}\right.\)

d.

$|2x+5|=|3x-7|$

\(\Leftrightarrow \left[\begin{matrix} 2x+5=3x-7\\ 2x+5=7-3x\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=12\\ x=0,4\end{matrix}\right.\)

e.

$|2x+7|=x-1\Rightarrow x-1\geq 0\Leftrightarrow x\geq 1$
Với $x\geq 1$ thì $|2x+7|=2x+7$

Khi đó pt trở thành:
$2x+7=x-1$

$\Leftrightarrow x=-8< 1$ (vô lý)

Vậy pt vô nghiệm.

g.

$|x-2|+|2x-3|=2$

Nếu $x\geq 2$ thì pt trở thành:

$x-2+2x-3=2$

$\Leftrightarrow 3x-5=2$

$\Leftrightarrow x=\frac{7}{3}$ (thỏa mãn)

Nếu $\frac{3}{2}\leq x< 2$ thì pt trở thành:

$2-x+2x-3=2$

$\Leftrightarrow x=3$ (không thỏa mãn)

Nếu $x< \frac{3}{2}$ thì pt trở thành:

$2-x+3-2x=2$

$\Leftrightarrow 5-3x=2$

$\Leftrightarrow x=1$ (thỏa mãn)

Vậy..........

h.

Từ đề suy ra $x\geq \frac{-2}{3}$

$\Rightarrow |x+2|=x+2$

Nếu  $x\geq 1$ thì $|1-x|=x-1$. PT trở thành:

$x+2+x-1=3x+2$

$\Leftrightarrow 2x+1=3x+2$

$\Leftrightarrow x=-1$ (vô lý)

Nếu $\frac{-2}{3}\leq x< 1$ thì $|1-x|=1-x$. PT trở thành:
$x+2+1-x=3x+2$

$\Leftrightarrow 3=3x+2$

$\Leftrightarrow x=\frac{1}{3}$ (thỏa mãn)

a: \(\left|7-2x\right|+7=2x\)

=>\(\left|2x-7\right|+7=2x\)

=>\(\left|2x-7\right|=2x-7\)

=>2x-7>=0

=>\(x>=\dfrac{7}{2}\)

b: \(\left|1-x\right|=4x+1\)

=>\(\left|x-1\right|=4x+1\)

=>\(\left\{{}\begin{matrix}4x+1>=0\\\left(4x+1\right)^2=\left(x-1\right)^2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{4}\\\left(4x+1\right)^2-\left(x-1\right)^2=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{4}\\\left(4x+1-x+1\right)\left(4x+1+x-1\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{4}\\5x\left(3x+2\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{1}{4}\\\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-\dfrac{2}{3}\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)

c: \(\left|x-\dfrac{1}{3}\right|+\dfrac{4}{5}=\left|3,2+\dfrac{2}{5}\right|\)

=>\(\left|x-\dfrac{1}{3}\right|=\dfrac{16}{5}+\dfrac{2}{5}-\dfrac{4}{5}=\dfrac{14}{5}\)

=>\(\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{14}{5}\\x-\dfrac{1}{3}=-\dfrac{14}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{14}{5}+\dfrac{1}{3}=\dfrac{42+5}{15}=\dfrac{47}{15}\\x=-\dfrac{14}{5}+\dfrac{1}{3}=\dfrac{-42+5}{15}=-\dfrac{37}{15}\end{matrix}\right.\)

d: \(\left|x-7\right|+2x+5=6\)

=>\(\left|x-7\right|=6-2x-5=-2x+1\)

=>\(\left\{{}\begin{matrix}-2x+1>=0\\\left(-2x+1\right)^2=\left(x-7\right)^2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x< =\dfrac{1}{2}\\\left(2x-1\right)^2-\left(x-7\right)^2=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x< =\dfrac{1}{2}\\\left(2x-1+x-7\right)\left(2x-1-x+7\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x< =\dfrac{1}{2}\\\left(3x-8\right)\left(x+6\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x< =\dfrac{1}{2}\\\left[{}\begin{matrix}x=\dfrac{8}{3}\left(loại\right)\\x=-6\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)

e: 3x-|2x-1|=2

=>|2x-1|=3x-2

=>\(\left\{{}\begin{matrix}3x-2>=0\\\left(3x-2\right)^2=\left(2x-1\right)^2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>=\dfrac{2}{3}\\\left(3x-2\right)^2-\left(2x-1\right)^2=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>=\dfrac{2}{3}\\\left(3x-2-2x+1\right)\left(3x-2+2x-1\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>=\dfrac{2}{3}\\\left(x-1\right)\left(5x-3\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{2}{3}\\\left[{}\begin{matrix}x-1=0\\5x-3=0\end{matrix}\right.\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>=\dfrac{2}{3}\\\left[{}\begin{matrix}x=1\left(nhận\right)\\x=\dfrac{3}{5}\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)

a, \(\left(2x-7\right)^2+\left(2x+7\right)^2-2\left(2x+7\right)\left(2x-7\right)=\left(2x-7-2x-7\right)^2=\left(-14\right)^2=196\)

b, \(\left(5x-3\right)^2-\left(5x+3\right)^2-15\left(2x-1\right)\)

\(=\left(5x-3-5x-3\right)\left(5x-3+5x+3\right)-15\left(2x-1\right)\)

\(=-6.10x-15\left(2x-1\right)\)

\(=-60x-15\left(2x-1\right)=-15\left(4x+2x-1\right)=-15\left(6x-1\right)=-90x+15\)

g: Ta có: \(3\left(2x-1\right)\left(3x-1\right)-\left(2x-3\right)\left(9x-1\right)=0\)

\(\Leftrightarrow3\left(6x^2-5x+1\right)-\left(18x^2-29x+3\right)=0\)

\(\Leftrightarrow18x^2-15x+3-18x^2+29x-3=0\)

\(\Leftrightarrow14x=0\)

hay x=0

w

\(\frac{2x+3}{2x+1}-\frac{2x+5}{2x+7}=1-\frac{6x^2+9x-9}{\left(2x+1\right)\left(2x+7\right)}\)

\(\Leftrightarrow1+\frac{2}{2x+1}-1-\frac{2}{2x+7}-1=-\frac{6x^2+9x-9}{\left(2x+1\right)\left(2x+7\right)}\)

\(\Leftrightarrow\frac{4x+14-4x-2+6x^2+9x-9}{\left(2x+1\right)\left(2x+7\right)}=1\)

\(\Leftrightarrow\frac{6x^2+9x+3}{\left(2x+1\right)\left(2x+7\right)}=1\)

\(\Leftrightarrow\frac{6x^2+6x+3x+3}{\left(2x+1\right)\left(2x+7\right)}=1\)

\(\Leftrightarrow\frac{6x\left(x+1\right)+3\left(x+1\right)}{\left(2x+1\right)\left(2x+7\right)}=1\)

\(\Leftrightarrow\frac{3\left(2x+1\right)\left(x+1\right)}{\left(2x+1\right)\left(2x+7\right)}=1\)

\(\Leftrightarrow3x+3=2x+7\)

\(\Leftrightarrow x=4\)

a: \(5^{\left(x-2\right)\left(x+3\right)}=1\)

=>\(\left(x-2\right)\left(x+3\right)=0\)

=>\(\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)

c: \(\left|x^2+2x\right|+\left|y^2-9\right|=0\)

mà \(\left\{{}\begin{matrix}\left|x^2+2x\right|>=0\forall x\\\left|y^2-9\right|>=0\forall y\end{matrix}\right.\)

nên \(\left\{{}\begin{matrix}x^2+2x=0\\y^2-9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(x+2\right)=0\\\left(y-3\right)\left(y+3\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x\in\left\{0;-2\right\}\\y\in\left\{3;-3\right\}\end{matrix}\right.\)

d: \(2^x+2^{x+1}+2^{x+2}+2^{x+3}=120\)

=>\(2^x\left(1+2+2^2+2^3\right)=120\)

=>\(2^x\cdot15=120\)

=>\(2^x=8\)

=>x=3

e: \(\left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\)

=>\(\left(x-7\right)^{x+11}-\left(x-7\right)^{x+1}=0\)

=>\(\left(x-7\right)^{x+1}\left[\left(x-7\right)^{10}-1\right]=0\)

=>\(\left[{}\begin{matrix}x-7=0\\x-7=1\\x-7=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=8\\x=6\end{matrix}\right.\)