Hãy đo rồi so sánh các đường chéo chính AD, BE và CF.

Những câu hỏi liên quan
Cho hình chữ nhật ABCD (Hình 1)
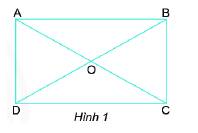
a) Đo rồi so sánh các cạnh và góc của hình chữ nhật.
b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không?
c) AC và BD được gọi là hai đường chéo của hình chữ nhật.
Hãy đo rồi so sánh AC và BD.
a) Các cạnh đối diện của hình chữ nhật bằng nhau (AB = CD = 4,5 cm, BC = AD = 2,5 cm).
Các góc của hình chữ nhật đều bằng nhau và bằng \( 90^0\)
b) AB và CD song song với nhau.
AD và BC song song với nhau.
c) AC và BD bằng nhau (cùng bằng 5,1 cm).
Đúng 0
Bình luận (0)
Cho hình thoi ABCD như Hình 4.
a) Hãy đo rồi so sánh các cạnh của hình thoi.
b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không?
c) AC và BD được gọi là hai đường chéo của hình thoi. Dùng êke để kiểm tra xem hai đường chéo có vuông góc với nhau hay không?
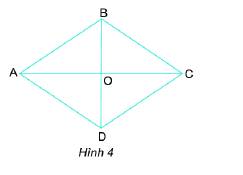
a) Các cạnh của hình thoi bằng nhau.
b) Kẻ đường thẳng qua B và vuông góc với BC. Đặt êke có góc vuông tại điểm cắt nhau giữa đường thẳng vừa kẻ và AD, đặt một cạnh góc vuông của êke trùng với đường thẳng ta thấy cạnh góc vuông còn lại của êke trùng khít với cạnh AD.
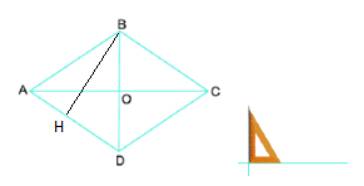
Khi đó BC và AD song song với nhau.
Tương tự AB và CD song song với nhau.
c) Tương tự như phần b, ta đặt đầu có góc vuông tại điểm O, đặt một cạnh góc vuông trùng với OB thì cạnh góc vuông còn lại trùng với OC hoặc OA. Khi đó AC và BD vuông góc với nhau.
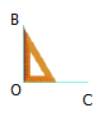
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD như Hình 7.a) Hãy đo rồi so sánh cạnh AB và CD; cạnh BC và AD.b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không?C) AC và BD được gọi là hai đường chéo của hình bình hành.Hai đường chéo AC và BD cắt nhau tại O. Hãy so sánh OA và OC; OB và OD.
Đọc tiếp
Cho hình bình hành ABCD như Hình 7.
a) Hãy đo rồi so sánh cạnh AB và CD; cạnh BC và AD.
b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không?
C) AC và BD được gọi là hai đường chéo của hình bình hành.
Hai đường chéo AC và BD cắt nhau tại O. Hãy so sánh OA và OC; OB và OD.
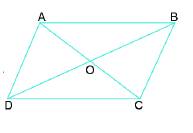
a) AB=CD; BC=AD.
b) Hai cặp cạnh AB và CD song song với nhau, BC và AD song song với nhau.
c) Sử dụng thước đo các cạnh ta thấy OA=OC; OB=OD.
Đúng 0
Bình luận (0)
Cho hình thang ABCD như Hình 9.a) Hãy đo rồi so sánh hai cạnh bên BC và AD.b) Hãy kiểm tra xem AB có song song với CD hay không?c) AC và BD được gọi là hai đường chéo. Hãy đo rồi so sánh AC và BD.
Đọc tiếp
Cho hình thang ABCD như Hình 9.
a) Hãy đo rồi so sánh hai cạnh bên BC và AD.
b) Hãy kiểm tra xem AB có song song với CD hay không?
c) AC và BD được gọi là hai đường chéo. Hãy đo rồi so sánh AC và BD.
a) Hai cạnh bên BC = AD (=3 cm).
b) AB song song với CD.
c) AC = BD (=4,8 cm).
Đúng 0
Bình luận (0)
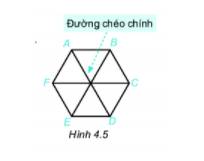
Hãy quan sát hình 4.5.
1. Hãy kể tên các đường chéo chính của hình lục giác đều ABCDEF.
2. Hãy so sánh độ dài các đường chéo chính với nhau.
1) Các đường chéo chính của hình: AD, BE, CF
2) Độ dài các đường chéo chính bằng hai lần độ dài cạnh của tam giác đều nên độ dài các đường chéo chính bằng nhau.
Đúng 1
Bình luận (0)
Cho D ABC nhọn (AB AC) nội tiếp đường tròn (O), Ba đường cao AD;BE; CF cắt nhau tại H. Hai đường cao BE; CF lần lượt cắt đường tròn tại điểm thứ hai là M và N. FD cắt BH tại K1) So sánh cung AB và cung AC2) Cho ∠ADB 550 Tính số đo cung BC3) Chứng minh tứ giác AEHF nội tiếp4)Chứng minh MN//EF5) Chứng minh HE.KB EF.KD6*) Cho BC cố định, A chạy trên cung lớn BC. Chứng minh độ dài AH; EF không đổi
Đọc tiếp
Cho D ABC nhọn (AB <AC) nội tiếp đường tròn (O), Ba đường cao AD;BE; CF cắt nhau tại H. Hai đường cao BE; CF lần lượt cắt đường tròn tại điểm thứ hai là M và N. FD cắt BH tại K
1) So sánh cung AB và cung AC
2) Cho ∠ADB = 550 Tính số đo cung BC
3) Chứng minh tứ giác AEHF nội tiếp
4)Chứng minh MN//EF
5) Chứng minh HE.KB = EF.KD
6*) Cho BC cố định, A chạy trên cung lớn BC. Chứng minh độ dài AH; EF không đổi
1: AB<AC
=>góc C<góc B
Xét (O) có
góc ACB=1/2*sđ cung AB
góc ABC=1/2*sđ cung AC
mà góc ACB<góc ABC
nên sđ cung AB<sđ cung AC
3: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
4:
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc HFE=góc HBC
=>góc HFE=góc HNM
mà hai góc này ở vị trí đồng vị
nên FE//MN
Đúng 0
Bình luận (0)
Dùng compa đo rồi so sánh độ dài hai đường chéo AC và BD.

Hai đường chéo bằng nhau.
Đúng 0
Bình luận (0)
Quan sát hình 4.3a.
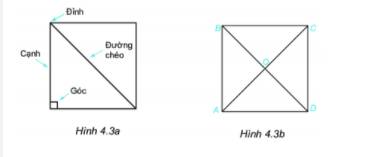
1. Nêu tên các đỉnh, cạnh, đường chéo của hình vuông ABCD (h.4.3b).
2. Dùng thước thẳng đo và so sánh độ dài các cạnh của hình vuông, hai đường chéo của hình vuông.
3. Dùng thước đo góc để đo và so sánh các góc của hình vuông.
1) Các đỉnh: A, B, C, D
Các cạnh: AB, BC, CD, DA
Các đường chéo: AC, BD
2) Độ dài các cạnh của hình vuông đều bằng nhau
Độ dài 2 đường chéo của hình vuông bằng nhau
3) Các góc của hình vuông đều bằng nhau và bằng 90o
Đúng 1
Bình luận (0)
cho lục giác abcdef có cặp cạnh đối song song và bằng nhau cmr các đường chéo ad,be,cf đồng qui





