\(n_{Fe}=a;n_{Cu}=b\\ 56a+64b=9,2\left(I\right)\\ BTe^{^{ }-}:3a+2b=2n_{SO_2}\left(II\right)\\ n_{H_2SO_4pư}=n_{SO_2}+1,5a+b\\ n_{H_2SO_4sau}=\dfrac{50.0,98}{98}-n_{SO_2}-1,5a-b=0,5-n_{SO_2}-1,5a-b\\ m_{ddsau}=9,2+50-64n_{SO_2}=59,2-64n_{SO_2}\\ \Rightarrow:\dfrac{98\left(0,5-n_{SO_2}-1,5a-b\right)}{59,2-64n_{SO_2}}=\dfrac{30,625}{100}\left(III\right)\\ \Rightarrow a=0,05;b=0,1;n_{SO_2}=0,175mol\\ V=0,175.22,4=3,92L\\ \%m_{Fe}=\dfrac{0,05.56}{9,2}.100\%=30,43\%\\ \%m_{Cu}=69,57\%\)

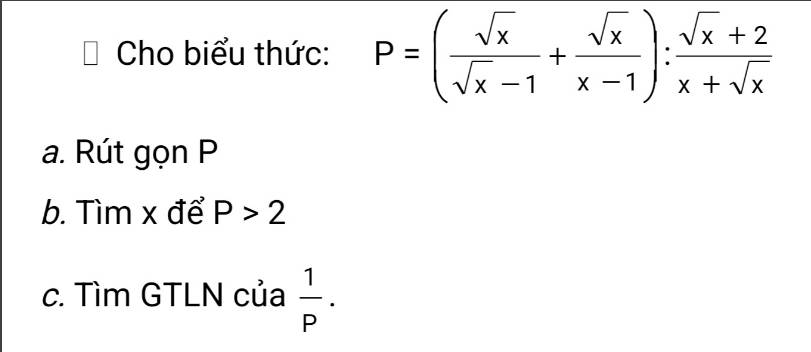
Lời giải:
a.  ĐKXĐ: $x>0; x\neq 1$

\(P=\left[\frac{\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}+\frac{\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}\right].\frac{x+\sqrt{x}}{\sqrt{x}+2}\)

\(=\frac{x+\sqrt{x}+\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{x}{\sqrt{x}-1}\)

b.

$P>2 \Leftrightarrow \frac{x}{\sqrt{x}-1}-2>0$

$\Leftrightarrow \frac{x-2\sqrt{x}+2}{\sqrt{x}-1}>0$

$\Leftrightarrow \frac{(\sqrt{x}-1)^2+1}{\sqrt{x}-1}>0$

$\Leftrightarrow \sqrt{x}-1>0$ (do $(\sqrt{x}-1)^2+1>0$)

$\Leftrightarrow x>1$

Kết hợp đkxđ suy ra $x>1$
c. 

$\frac{1}{P}=\frac{\sqrt{x}-1}{x}$

Áp dụng BĐT Cô-si:

$x+4\geq 4\sqrt{x}\Rightarrow x\geq 4(\sqrt{x}-1)$
$\Rightarrow \frac{\sqrt{x}-1}{x}\leq \frac{\sqrt{x}-1}{4(\sqrt{x}-1)}=\frac{1}{4}$

Vậy $\frac{1}{P}$ max $=\frac{1}{4}$ khi $x=4$

C2 cug cơ bản tự làm nhee

Câu 1:

\(n_{Ca\left(OH\right)_2}=1,8.0,05=0,09\left(mol\right)\)

BTNT Ca, có: \(n_{CaCO_3}=n_{Ca\left(OH\right)_2}=0,09\left(mol\right)\)

Mà: m_CaCO3 + m_BaCO3 = 18,85 (g)

\(\Rightarrow n_{BaCO_3}=\dfrac{18,85-0,09.100}{197}=0,05\left(mol\right)\)

BTNT C, có: n_CO2 = n_CaCO3 + n_BaCO3 = 0,14 (mol) = n_C

Sau pư với Ca(OH)₂ có: \(\left\{{}\begin{matrix}n_{CaCO_3}+2n_{Ca\left(HCO_3\right)_2}=0,14\\n_{CaCO_3}+n_{Ca\left(HCO_3\right)_2}=0,09\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}n_{CaCO_3}=0,04\left(mol\right)\\n_{Ca\left(HCO_3\right)_2}=0,05\left(mol\right)\end{matrix}\right.\)

Có: m _{dd tăng} = m_CO2 + m_H2O - m _{kết tủa}

⇒ 3,78 = 0,14.44 + 18n_H2O - 0,04.100 ⇒ n_H2O = 0,09 (mol)

⇒ n_H = 0,09.2 = 0,18 (mol)

\(\Rightarrow n_N=\dfrac{2,14-0,14.12-0,18.1}{14}=0,02\left(mol\right)\)

Gọi: CTPT của A là C_xH_yN_t

⇒ x:y:t = 0,14:0,18:0,02 = 7:9:1

Vậy: CTĐGN của A là C₇H₉N.

Câu 2:

X gồm C, H và N, có thể có O.

Ta có: \(n_{CO_2}=\dfrac{4,48}{22,4}=0,2\left(mol\right)=n_C\)

\(\Rightarrow\%m_C=\dfrac{0,2.12}{7,7}.100\%\approx31,2\%\)

⇒ %m_O = 100 - 31,2 - 9,09 - 18,18 = 41,53%

→ X gồm: C, H, O và N.

Gọi CTPT của X là C_xH_yO_zN_t.

⇒ x:y:z:t = \(\dfrac{31,2}{12}:\dfrac{9,09}{1}:\dfrac{41,53}{16}:\dfrac{18,18}{14}=2:7:2:1\)

→ X có CTPT dạng: (C₂H₇O₂N)_n.

Mà: M_X < 78 \(\Rightarrow\left(12.2+7+16.2+14\right)n< 78\)

\(\Rightarrow n< 1,01\) ⇒ n = 1

Vậy: X là C₂H₇O₂N.

Bài 4:

(1): \(x^2-x-5=0\)

a=1;b=-1;c=-5

Vì a*c=-5<0

nên (1) có hai nghiệm phân biệt trái dấu

Theo Vi-et, ta được: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-1\right)}{1}=1\\x_1\cdot x_2=\dfrac{c}{a}=-5\end{matrix}\right.\)

\(\left(\left|x_1\right|-\left|x_2\right|\right)^2=x_1^2+x_2^2-2\left|x_1\cdot x_2\right|\)

\(=\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|\)

\(=1^2-2\cdot\left(-5\right)-2\left|-5\right|=1+10-10=1\)

=>\(\left[{}\begin{matrix}\left|x_1\right|-\left|x_2\right|=1\\\left|x_1\right|-\left|x_2\right|=-1\end{matrix}\right.\)

TH1: \(\left|x_1\right|-\left|x_2\right|=1\)

=>\(\dfrac{\left|x_1\right|-\left|x_2\right|}{x_1+x_2}=\dfrac{1}{1}=1;\dfrac{x_1+x_2}{x_1x_2}=\dfrac{1}{-5}=-\dfrac{1}{5}\)

\(\dfrac{\left|x_1\right|-\left|x_2\right|}{x_1+x_2}\cdot\dfrac{x_1+x_2}{x_1x_2}=1\cdot\dfrac{-1}{5}=-\dfrac{1}{5}\)

\(\dfrac{\left|x_1\right|-\left|x_2\right|}{x_1+x_2}+\dfrac{x_1+x_2}{x_1x_2}=1-\dfrac{1}{5}=\dfrac{4}{5}\)

Phương trình bậc hai lập được sẽ là: \(a^2-\dfrac{4}{5}a-\dfrac{1}{5}=0\)

TH2: \(\left|x_1\right|-\left|x_2\right|=-1\)

=>\(\dfrac{\left|x_1\right|-\left|x_2\right|}{x_1+x_2}=\dfrac{-1}{1}=-1;\dfrac{x_1+x_2}{x_1x_2}=\dfrac{1}{-5}=-\dfrac{1}{5}\)

\(\dfrac{\left|x_1\right|-\left|x_2\right|}{x_1+x_2}\cdot\dfrac{x_1+x_2}{x_1x_2}=-1\cdot\dfrac{-1}{5}=\dfrac{1}{5}\)

\(\dfrac{\left|x_1\right|-\left|x_2\right|}{x_1+x_2}+\dfrac{x_1+x_2}{x_1x_2}=-1+\dfrac{1}{5}=-\dfrac{4}{5}\)

Phương trình bậc hai lập được sẽ là: \(a^2+\dfrac{4}{5}a+\dfrac{1}{5}=0\)

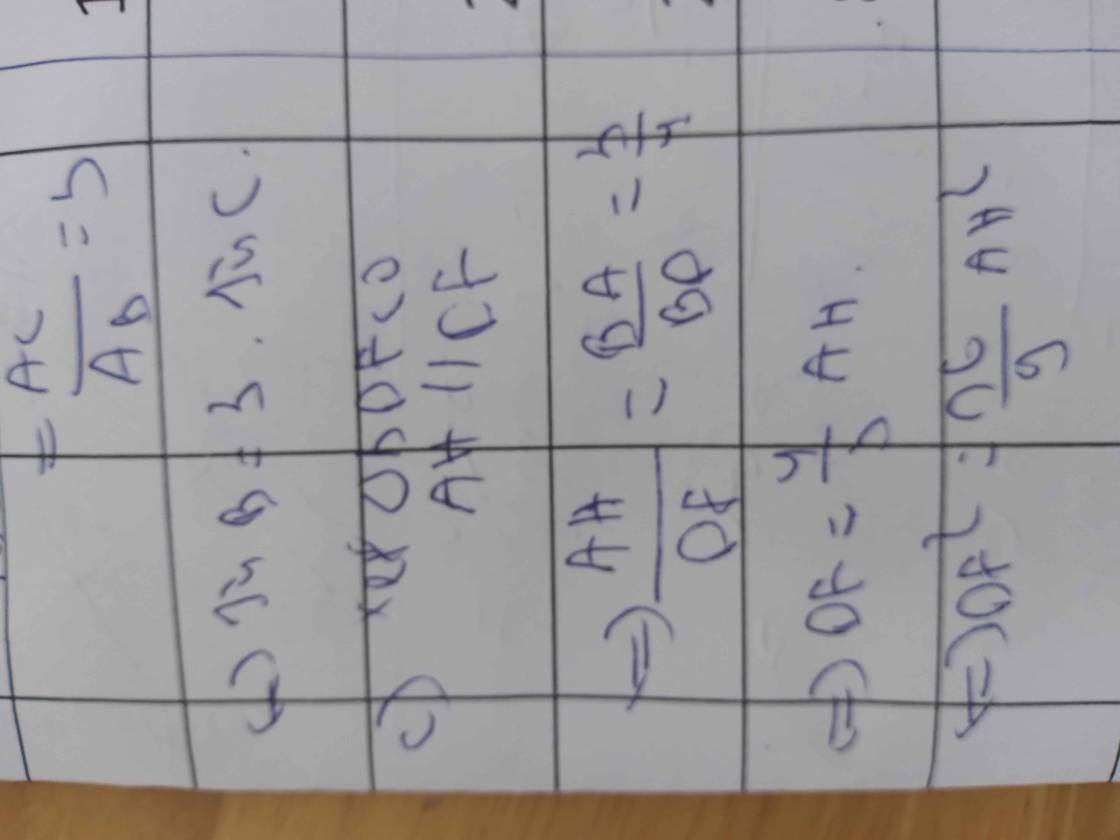
a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=30^0\)

Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)

=>\(\dfrac{4}{BC}=sin30=\dfrac{1}{2}\)

=>BC=8(cm)

\(AC=\sqrt{BC^2-AB^2}=4\sqrt{3}\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên AH*BC=AB*AC

=>\(AH\cdot8=4\cdot4\sqrt{3}=16\sqrt{3}\)

=>\(AH=2\sqrt{3}\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{4^2}{8}=2\left(cm\right)\\CH=\dfrac{48}{8}=6\left(cm\right)\end{matrix}\right.\)

b: \(BC\cdot sinB\cdot sinC\)

\(=BC\cdot\dfrac{AC}{BC}\cdot\dfrac{AB}{BC}=\dfrac{AB\cdot AC}{BC}=AH\)

\(BC\cdot cos^2B\)

\(=BC\cdot\left(\dfrac{AB}{BC}\right)^2=\dfrac{AB^2}{BC}=BH\)

\(BC\cdot sin^2B=BC\cdot\left(\dfrac{AC}{BC}\right)^2=\dfrac{AC^2}{BC}=CH\)

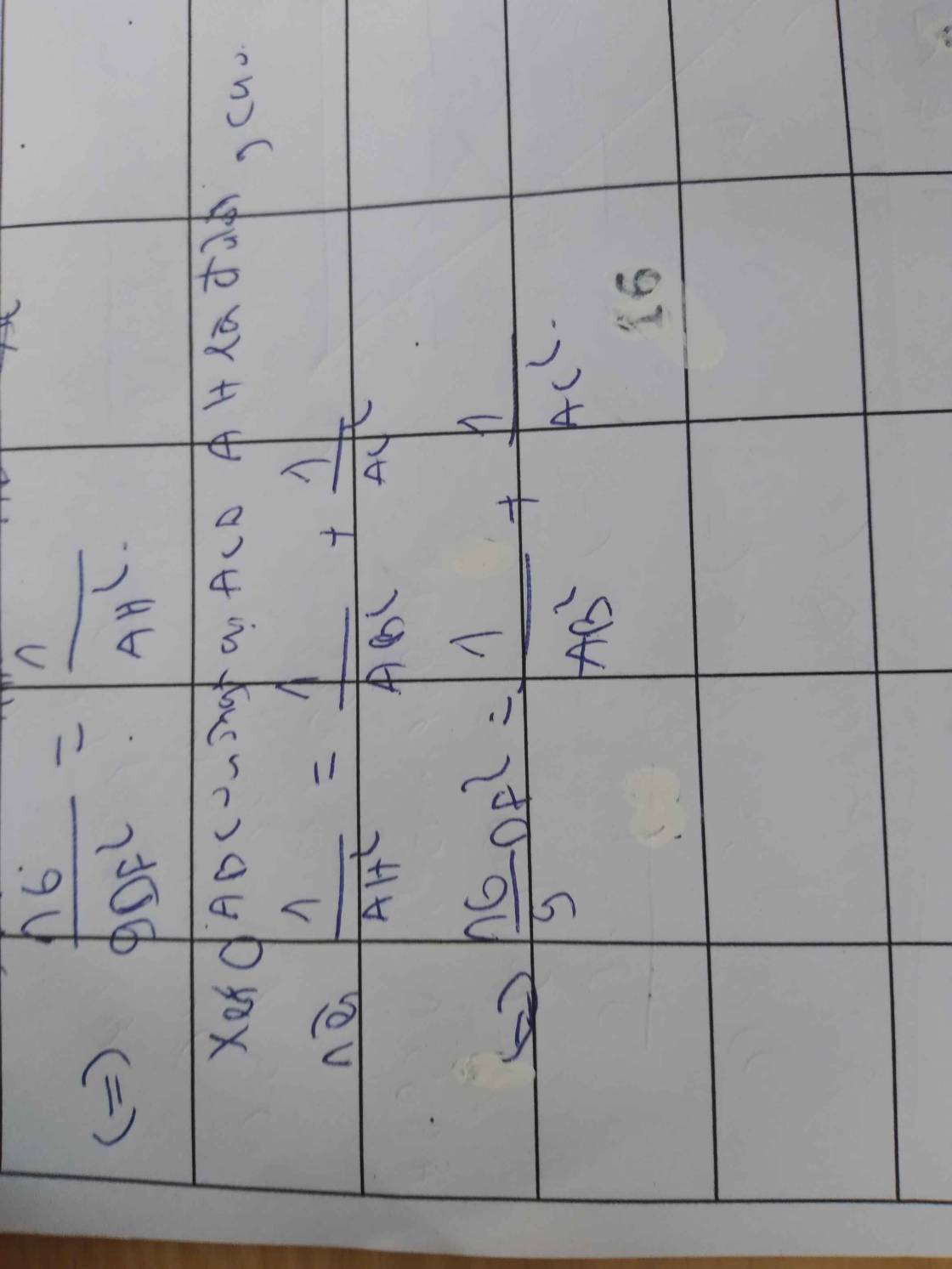
c:

\(\dfrac{AH^2}{AC^2}=\dfrac{HB\cdot HC}{BC\cdot HC}=\dfrac{HB}{BC}\)

ΔHAB vuông tại H có HD là đường cao

nên \(\left\{{}\begin{matrix}BD\cdot BA=BH^2\\AD\cdot AB=AH^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=\dfrac{BH^2}{AB}\\AD=\dfrac{AH^2}{AB}\end{matrix}\right.\)

ΔHAC vuông tại H có HE là đường cao

nên \(\left\{{}\begin{matrix}CE\cdot CA=CH^2\\AE\cdot AC=AH^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}CE=\dfrac{CH^2}{AC}\\AE=\dfrac{AH^2}{AC}\end{matrix}\right.\)

\(\dfrac{DB}{EC}=\dfrac{HB^2}{AB}:\dfrac{HC^2}{AC}\)

\(=\dfrac{HB^2}{AB}\cdot\dfrac{AC}{HC^2}\)

\(=\left(\dfrac{HB}{HC}\right)^2\cdot\dfrac{AC}{AB}=\dfrac{AC}{AB}\cdot\left(\dfrac{AB}{AC}\right)^4=\left(\dfrac{AB}{AC}\right)^3\)

\(BD\cdot CE\cdot BC\)

\(=\dfrac{BH^2}{AB}\cdot\dfrac{CH^2}{AC}\cdot BC\)

\(=\dfrac{AH^4}{AH}=AH^3\)

=DE³

\(BC\cdot HD\cdot HE\)

\(=BC\cdot\dfrac{HA\cdot HB}{AB}\cdot\dfrac{HA\cdot HC}{AC}\)

\(=\dfrac{1}{AH}\cdot\dfrac{HA^2\cdot HB\cdot HC}{1}=\dfrac{HA\cdot HB\cdot HC}{1}=HA^3\)

\(=DE^3\)

=>ĐPCM

a:Xét  ΔOHB vuông tại H có HM là đường cao

nên \(OM\cdot OB=OH^2\left(1\right)\)

Xét ΔOHC vuông tại H có HN là đường cao

nên \(ON\cdot OC=OH^2\left(2\right)\)

Từ (1) và (2) suy ra \(OM\cdot OB=ON\cdot OC\)

\(OM\cdot OB=OH^2\)

=>\(OM\cdot OB=OA^2\)

=>\(\dfrac{OM}{OA}=\dfrac{OA}{OB}\)

Xét ΔOMA và ΔOAB có

\(\dfrac{OM}{OA}=\dfrac{OA}{OB}\)

\(\widehat{MOA}\) chung

Do đó: ΔOMA đồng dạng với ΔOAB

=>\(\widehat{MAO}=\widehat{OBA}\)

=>\(\widehat{MAO}=\widehat{MOA}\)

=>MO=MA

=>M nằm trên đường trung trực của AO

ON*OC=OA²

=>ON/OA=OA/OC

Xét ΔONA và ΔOAC có

\(\dfrac{ON}{OA}=\dfrac{OA}{OC}\)

\(\widehat{NOA}\) chung

Do đó: ΔONA đồng dạng với ΔOAC
=>\(\widehat{ONA}=\widehat{OAC}=\widehat{NAO}\)

=>\(\widehat{NAO}=\widehat{NOA}\)

=>NA=NO

=>N nằm trên đường trung trực của AO

=>MN là đường trung trực của AO

=>MN luôn đi qua O

b:

Gọi D là giao điểm của OA và MN

=>OA\(\perp\)MN tại D

 \(OM\cdot OB=ON\cdot OC\)

=>\(\dfrac{OM}{ON}=\dfrac{OC}{OB}\)

=>\(\dfrac{OM}{OC}=\dfrac{ON}{OB}\)

Xét ΔOMN và ΔOCB có

\(\dfrac{OM}{OC}=\dfrac{ON}{OB}\)

\(\widehat{MON}\) chung

Do đó: ΔOMN đồng dạng với ΔOCB

OH\(\perp\)BC

OD\(\perp\)MN

=>\(\dfrac{OM}{OD}=\dfrac{OC}{OH}\)

=>\(\dfrac{OM}{\dfrac{R}{2}}=\dfrac{OC}{R}\)

=>\(OM=\dfrac{1}{2}OC\)

\(OM\cdot OB=OH^2\)

=>\(\dfrac{1}{2}\cdot OC\cdot OB=R^2\)

=>\(OB\cdot OC=2R^2\)