Tứ giác: 0 trục, 0 tâm

Hình thang 0 trục, 0 tâm

Hình thang cân 1 trục 0 tâm

Hình bình hành 0 trục 1 tâm

Hình chữ nhật 2 trục 1 tâm

Hình thoi 2 trục 1 tâm

Hình vuông 4 trục 1 tâm

Tứ giác: 0 trục đối xứng, 0 tâm đối xứng

Hình thang: 0 trục đối xứng, 0 tâm đối xứng

Hình thang cân: 1 trục đối xứng, 0 tâm đối xứng

Hình bình hành: 0 trục đối xứng, 1 tâm đối xứng

Hình chữ nhật: 2 trục đối xứng, 1 tâm đối xứng

Hình thoi: 2 trục đối xứng, 1 tâm đối xứng

Hình vuông: 4 trục đối xứng, 1 tâm đối xứng

Tích đúng 5 sao cho mình nhé. 

OK bạn

D

d 

C

B

B. Hình Chữ Nhật 

B

a)

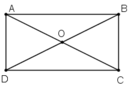
Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.

Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

Vậy: OA = OC và OB= OD

Do đó, O là tâm đối xứng của hình chữ nhật đó.

b)

Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.

ABCD là hình chữ nhật

⇒ ABCD là hình thang cân (hai đáy AB và CD)

⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.

Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC

⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.

Vậy ta có điều phải chứng minh.

a) Vì hình bình hành nhận giao điểm hai đường chéo làm tâm đối xứng, mà hình chữ nhật là một hình bình hành nên giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình.

b) Vì hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cần có đáy là hai cạnh đối xứng của hình chữ nhật là trục đối xứng của hình

a) Vì hình bình hành nhận giao điểm hai đường chéo làm tâm đối xứng, mà hình chữ nhật là một hình bình hành nên giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình.

b) Vì hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cần có đáy là hai cạnh đối xứng của hình chữ nhật là trục đối xứng của hình.

Câu 2:

\(a,\) Chiều dài là \(4.3=12(m)\)

Diện tích là \(4.12=48(m^2)\)

\(b,48(m^2)=480000(cm^2)\)

Số viên gạch cần để lát là \(480000:(40.40)=300(\text{viên gạch})\)

Vậy cần \(300.18000=5400000(đồng)\)

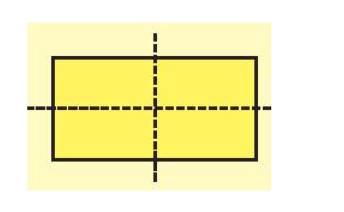
+) Trục đối xứng của hình chữ nhật là đường thẳng đi qua trung điểm hai cạnh đối diện vì khi gấp theo đường đó thì ta được hai hình chữ nhật chồng khít lên nhau.

+) Ta tìm được hai trục đối xứng.

a,Vì hình bình hành nhận giao điểm hai đường chéo làm tâm đối xứng, mà hình chữ nhật là một hình bình hành nên giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình

b,Vì hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà  hình chữ nhật là một hình thang cân có hai đáy là hai cạnh đối xứng của hình chữ nhật nên hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó


 

a) Do trong hình chữ nhật, hai đường chéo cắt nhau tại trung điểm mỗi đường nên giao điểm của hai đường chéo là tâm đối xứng của hình chữ nhật.

b) Do hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cân có đáy là hai cạnh đối xứng của hình chữ nhật, do đó hai đường thẳng đi qua trung điểm hai cạnh đối của hình chữ nhật là trục đối xứng của hình.

a) Do trong hình chữ nhật, hai đường chéo cắt nhau tại trung điểm mỗi đường nên giao điểm của hai đường chéo là tâm đối xứng của hình chữ nhật.

b) Do hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cân có đáy là hai cạnh đối xứng của hình chữ nhật, do đó hai đường thẳng đi qua trung điểm hai cạnh đối của hình chữ nhật là trục đối xứng của hình.