Đáp án D.

+) Xét △ABC có MN là đường trung bình ⇒MN//AC

Mà MN∈ (SMN) ⇒AC// (SMN)

+) Xét △SMN có \(\dfrac{SG1}{SM}\)=\(\dfrac{SG2}{SN}\)=\(\dfrac{2}{3}\)( Tính chất trọng tâm)

⇒G1G2//MN  ⇒ G1G2//AC ( Vì AC//MN)

Mà AC∈(SAC) ⇒ G1G2// (SAC)

Do IJ là đường thẳng trung bình của hình thang ABCD nên IJ // AB. Hai mặt phẳng (GIJ) và (SAB) lần lượt chứa hai đường thẳng song song nên giao tuyến của chúng là đường thẳng đi qua G và song song với AB. Đường thẳng này cắt SA tại điểm M và cắt SB tại N. vậy thiết diện là hình thang MIJN, với M, N là giao điểm của đường thẳng đi qua G và song song với AB với hai đường thẳng SA, SB.

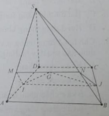
Đáp án B.

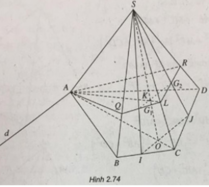
Gọi I, J lần lượt là trung điểm của BC, CD.

Ta có I J   / /   G 1 G 2  nên giao tuyến của hai mặt phẳng ( A G 1 G 2 ) và (ABCD) là đường thẳng d qua A và song song với IJ

Gọi O = IJ ∩ AC, K   =   G 1 G 2   ∩   S O , L = AK ∩ SC

L G 2  cắt SD tại R

L G 2  cắt SB tại Q

Ta có thiết diện là tứ giác AQLR.

Đáp án D

Trong mp(SDA), gọi E là giao điểm của SG với AD

Trong mp(SBC), gọi K là giao điểm của SH với BC

Xét ΔSAD có

G là trọng tâm của ΔSAD
E là giao điểm của SG với AD

Do đó: E là trung điểm của AD

Xét ΔSBC có

H là trọng tâm của ΔSBC

SH cắt BC tại K

Do đó: K là trung điểm của BC

Xét hình thang ABCD(AB//CD) có

E,K lần lượt là trung điểm của AD,BC

=>EK là đường trung bình

=>EK//AB

Xét ΔSDE có

SE là đường trung tuyến

G là trọng tâm

Do đó: \(\dfrac{SG}{SE}=\dfrac{2}{3}\)

Xét ΔSBC có

H là trọng tâm của ΔSBC

SK là đường trung tuyến

Do đó: \(\dfrac{SH}{SK}=\dfrac{2}{3}\)

Xét ΔSEK có \(\dfrac{SG}{SE}=\dfrac{SH}{SK}\left(=\dfrac{2}{3}\right)\)

nên GH//EK

mà EK//AB

nên GH//AB

Ta có: GH//AB

AB\(\subset\)(SAB)

GH không nằm trong mp(SAB)

Do đó: GH//(SAB)

Đáp án A

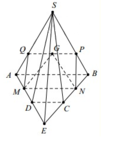
Qua G kẻ đường thẳng d song song với AB và cắt SA, SB lần lượt tại hai điểm Q, P. Vì MN là đường trung bình của ABCD ⇒ MN//AB

Do đó MN//PQ. Vậy giao tuyến của mặt phẳng (MNG) và (SAB) là PQ.

Mặt phẳng (MNG) cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ

Vì MN//PQ suy ra MNPQ là hình thang

Để MNPQ là hình bình hành  ⇔ MN=PQ (1)

Gọi I là trung điểm của AB, G là trọng tâm tam giác  S A B ⇒ S G S I = 2 3

Tam giác SAB có  P Q / / A B ⇒ P Q A B = S G S I = 2 3 ⇔ P Q = 2 3 A B (2)

Mà MN là đường trung bình  hình thang  A B C D ⇒ M N = A B + C D 2 (3)

Từ (1) , (2) và (3) suy ra 2 3 A B = A B + C D 2 ⇔ 4 A B = 3 A B + 3 C D ⇔ A B = 3 C D .