a) Tính khoảng cách từ gốc toạ độ C(0;0) đến điểm M(3 ; 4) trong mặt phẳng toạ độ Oxy.
b) Cho hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy. Nêu công thức tính độ dài đoạn thẳng IM.
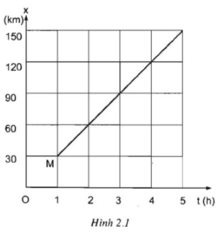
Hình 2.1 là đồ thị toạ độ - thời gian của môt chiếc ô tô chay từ A đến B trên một đường thẳng. Điểm A cách gốc toạ độ bao nhiêu kilômét ? Thời điểm xuất phát cách mốc thời gian mấy giờ ?
A. A trùng với gốc toạ độ o, xe xuất phát lúc 0 h, tính từ mốc thời gian.
B. A trùng với gốc toạ độ o, xe xuất phát lúc 1 h, tính từ mốc thời gian.
C. A cách gốc o 30 km, xe xuất phát lúc 0 h.
D. A cách gốc o 30 km, xe xuất phát lúc 1 h.
a) Gọi đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=a'x+b'\)
Vì \(\left(d'\right)//\left(d\right)\Rightarrow a'=2\)
Vậy phương trình đường thẳng (d') có dạng \(\left(d'\right):y=2x+b'\)
Mặt khác (d') đi qua M(3;4) nên điểm M(3;4) thuộc \(\left(d'\right):y=2x+b'\)
Thay \(x=3;y=4\)vào hàm số \(y=2x+b'\)ta có:
\(4=2.3+b'\Leftrightarrow b'=-2\)
Vậy phương trình đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=2x-2\)
b) Gọi OH là khoảng cách từ O đến (d). Gọi giao điểm của (d):y = 2x + 6 với hai trục Ox, Oy lần lượt là A(xA;0), B(0;yB).
Thay x = xA; y = 0 vào hàm số y = 2x + 6, ta có: \(0=2x_A+6\Leftrightarrow x_A=-3\)
Thay x = 0; y = yB vào hàm số y = 2x + 6, ta có: \(y_B=2.0+6=6\)
Vì \(OA=\left|x_A\right|;OB=\left|y_B\right|\)\(\Rightarrow OA=\left|-3\right|=3;OB=\left|6\right|=6\)
\(\Delta OAB\)vuông tại O, đường cao OH \(\Rightarrow\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\left(htl\right)\)
Rồi bạn thay OA, OB vào và dễ dàng tính được OH
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi thoả mãn a + b + c = 3 Khoảng cách từ gốc toạ độ O đến mặt phẳng (ABC) có giá trị lớn nhất bằng
A. 3
B. 1 3
C. 3 3
D. 3 3
Có ![]()
![]() và tứ diện O.ABC vuông tại O nên:
và tứ diện O.ABC vuông tại O nên:
![]()

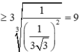
![]()
Chọn đáp án B. Mẹo TN: Vì tính đối xứng cho

![]()
Chọn đáp án B.
Cho đường thẳng d có phương trình tổng quát là: x - 2y – 5 = 0.
a) Lập phương trình tham số của đường thẳng d.
b) Tìm toạ độ điểm M thuộc d sao cho OM = 5 với O là gốc toạ độ.
c) Tìm toạ độ điểm N thuộc d sao cho khoảng cách từ N đến trục hoành Ox là 3.
a) Từ phương trình tổng quát của đường thẳng, ta lấy được một vecto pháp tuyến là: \(\overrightarrow n = \left( {1; - 2} \right)\) nên ta chọn vecto chỉ phương của đường thẳng d là: \(\overrightarrow u = \left( {2;1} \right)\).
Chọn điểm \(A\left( {1; - 2} \right) \in d\).Vậy phương trình tham số của đường thẳng d là: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\end{array} \right.\) (t là tham số)
b) Do điểm M thuộc d nên ta có: \(M\left( {1 + 2m; - 2 + m} \right);m \in \mathbb{R}\).
Ta có: \(OM = 5 \Leftrightarrow \sqrt {{{\left( {1 + 2m} \right)}^2} + {{\left( { - 2 + m} \right)}^2}} = 5 \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2\)
Với \(m = 2 \Rightarrow M\left( {5;0} \right)\)
Với \(m = - 2 \Rightarrow M\left( { - 3; - 4} \right)\)
Vậy ta có 2 điểm M thỏa mãn điều kiện đề bài.
c) Do điểm N thuộc d nên ta có: \(N\left( {1 + 2n; - 2 + n} \right)\)
Khoảng cách từ N đến trục hoành bằng giá trị tuyệt đối của tung độ điểm N. Do đó, khoảng cách tư N đến trục hoành bằng 3 khi và chỉ khi: \(\left| { - 2 + n} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = - 1\end{array} \right.\)
Với \(n = 5 \Rightarrow N\left( {11;3} \right)\)
Với \(n = - 1 \Rightarrow N\left( { - 1; - 3} \right)\)
Vậy có 2 điểm N thỏa mãn bài toán
GIÚP VỚI Ạ!! Cho hàm số y = −2x + 4 .
a. Vẽ đồ thị (d) của hàm số.
b. Tính khoảng cách từ gốc toạ độ O đến (d) và diện tích tam giác tạo bởi (d) và hai trục toạ độ.
Cho đường thẳng d có phương trình : y = kx +3
a ) chứng minh rằng đường thẳng d luôn đi qua một điểm cố định khi k thay đổi
b) Tính giá trị cảu k để khoảgn cách từ gốc toạ độ O tới đường thẳng d bằng 2
c) tìm giá trị của k để khoảng cách từ gốc toạ độ O tới đường thẳng d lớn nhất
làm hộ mình với mình tick cho hihi
y = kx +3 <=>kx+3-y=0 => x=0,y=3
đường thẳng d luôn đi qua một điểm cố định(0;3)
b)khoảgn cách từ gốc toạ độ O tới đường thẳng d bằng căn 2 của x^2+y^2
=>x^2+y^2=4 (1)
Thế y = kx +3, \(x^2+\left(kx+3\right)^2=4\)
\(x^2\left(1+k^2\right)+6kx+5=0\)có nghiệm khi k>=\(\frac{\sqrt{5}}{3}\)
c)
Một châts điểm chuyển động từ điểm A đến B cách nhau 90km với tốc độ là 30km/h trên trục OX biết chất điểm đó cách gốc toạ độ một khoảng 30km chiều dương từ A đến B O là gốc toạ độ. a)viết phương trình toạ độ
cho đương thẳng (d):y=x+2 khoảng cách từ gốc toạ độ đến đường thẳng(d) là?
Gọi A và B lần lượt là giao điểm của d với Ox và Oy
\(\Rightarrow A\left(-2;0\right)\) và \(B\left(0;2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA=\left|x_A\right|=2\\OB=\left|y_B\right|=2\end{matrix}\right.\)
\(\Rightarrow\Delta OAB\) vuông cân tại O
Gọi H là hình chiếu vuông góc của O lên d \(\Rightarrow OH=d\left(O;d\right)\)
Mặt khác do OAB vuông cân \(\Rightarrow\) OH là đường cao đồng thời là trung tuyến
\(\Rightarrow OH=\dfrac{1}{2}BC=\dfrac{1}{2}\sqrt{OA^2+OB^2}=\sqrt{2}\)
cho đường thẳng (d) : y=X+2 khoảng cách từ gốc tọa độ đến đường thẳng (d) là
Bài 5: Cho (d): y = -2x + 3
a) Tìm tọa độ giao điểm A, B của ĐTHS lần lượt với Ox, Oy
b) Tính khoảng cách từ gốc tọa độ đến đường thẳng (d)
c) Tính khoảng cách từ C(0; -2) đến đường thẳng (d)
\(a,\) Pt hoành độ giao điểm
\(x=0\\ \Leftrightarrow y=-2\cdot0+3=3\\ \Leftrightarrow A\left(0;3\right)\)
Pt tung độ giao điểm
\(y=0\\ \Leftrightarrow0=-2x+3\Leftrightarrow x=\dfrac{3}{2}\\ \Leftrightarrow B\left(\dfrac{3}{2};0\right)\)