cho tam giác ABc có đường cao BD=6cm;độ dài trung tuyến CE=5cm.khoảng giao điểm BD với CE đến AC=1cm. tìm độ dài cạnh AB

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB=6cm;BC=10cm đường cao AH
a.CM tam giác ABC đồng dạng với tam giác HAC và AC2 = CH.BC
b.Tính độ dài AC,AH
c.Vẽ đường phân giác BD cắt AH,AC lần lượt tại I,K.CM AI2=IH.CK
a) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACB}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
Suy ra: \(\dfrac{AC}{HC}=\dfrac{BC}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AC^2=CH\cdot BC\)(đpcm)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông A có AB=6cm, BC=10cm, đường phân giác BD Kẻ DH vuông góc BC
1, tính tỉ số đường cao AD/CD
2, Cm AB. DC=HD.BC
3, Tính diện tích tam giác DHC
1: Xét ΔABC có BD là đường phân giác
nên AD/CD=AB/BC=3/5
2: Xét ΔCHD vuông tại H và ΔCAB vuông tại A có
\(\widehat{C}\) chung
do đó: ΔCHD∼ΔCAB
Suy ra: HD/AB=CD/CB
hay \(CD\cdot AB=HD\cdot CB\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC, có AB = 6cm, BC = 10cm. Các đường phân giác trong và ngoài của góc B cắt AC lần lượt tại D và E. Tính BD và BE.
Bài 2: Cho tam giác ABC vuông tại A, đường phân giác trong AD, đường cao AH, CD = 68cm, BD = 51cm. Tính BH
Cho tam giác ABC AB nhỏ hơn AC , có 3 góc nhọn và đường cao AH. Qua H vẽ HM vuông góc với AC tại M và HN vuông góc với AC tại N.a Cho AC 6cm, AM 3cm. Chứng minh diện tích tam giác ACB gấp 4 lần tam giác AMNb Vẽ đường cao BD của tam giác ABC cắt AH tại E. Qua D vẽ đường thẳng song song với MN cắt AB tại F. Chứng minh góc AEF = ABC
cho tam giác ABC có đường cao BD=6cm;độ dài trung tuyến CE=5cm.KHoảng giao điểm BD đến AC bằng 1cm. tính độ dài cạnh AB
cho tam giác ABc có đường cao BD=6cm;độ dài trung tuyến CE=5cm.khoảng giao điểm BD với CE đến AC=1cm. tìm độ dài cạnh AB
Cho tam giác ABC, biết AB=6cm, AC=8cm, BC=8cm. Vẽ đường cao AH, đường phân giác BD cắt nhau tại I.Cm ID/BD+IH/AH+IE/CE=1
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD. Chọn kết luận đúng.
A. AD = 6cm
B. DC = 5cm
C. AD = 5cm
D. BC = 12cm
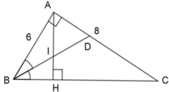
+ Áp dụng định lý Pitago trong tam giác vuông ABC ta có:
A B 2 + A C 2 = B C 2 ⇔ 6 2 + 8 2 = B C 2 ⇔ B C 2 = 100 ⇒ B C = 10 c m
+ Vì BD là đường phân giác của tam giác ABC nên áp dụng tính chất đường phân giác của tam giác, ta có:
B A A D = B C C D ⇔ B A A D = B C C A − A D ⇔ 6 A D = 10 8 − A D
=> AD = 3cm => DC = AC - AD = 8 - 3 = 5cm
Đáp án: B
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A, AB 6cm, AC 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD. Chọn khẳng định đúng. A. AB.BI BD.HB B.
A
B
.
B
I
A
I
2
C.
A
B
.
B
I
B
D
2
D.
A
B
.
B
I
H
I...
Đọc tiếp
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD. Chọn khẳng định đúng.
A. AB.BI = BD.HB
B. A B . B I = A I 2
C. A B . B I = B D 2
D. A B . B I = H I 2
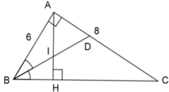
Xét 2 tam giác vuông ABD và HBI có:
A B D ^ = H B I ^ (BD là tia phân giác của góc B)
=> ΔABD ~ ΔHBI (g - g)
⇒ A B H B = B D B I ⇔ AB.BI = BD.HB
Đáp án: A
Đúng 0
Bình luận (0)










