Xác định điểm N trên đường tròn lượng giác sao cho \(\left( {OA,ON} \right) = - \frac{\pi }{3}\)

Những câu hỏi liên quan
Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác \(\left( {OA,OM} \right),\,\left( {OA,ON} \right),\,\left( {OA,OP} \right)\) lần lượt bằng \(\frac{\pi }{2};\,\,\frac{{7\pi }}{6};\,\, - \frac{\pi }{6}\). Chứng minh rằng tam giác MNP là tam giác đều.
Tham khảo:
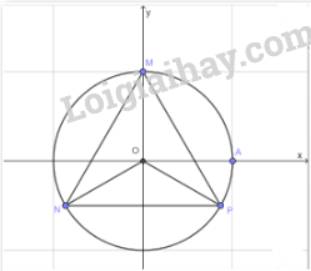
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều
Đúng 0
Bình luận (0)
Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = x\left( {rad} \right)\) (Hình 23). Hãy xác định \(\sin x\).
\(\sin x = \frac{{OK}}{{OM}}\)
Đúng 0
Bình luận (0)
Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = x\left( {rad} \right)\) (Hình 26). Hãy xác định \(\cos x\)
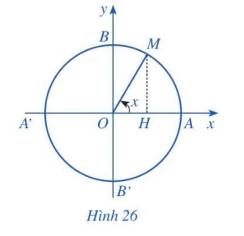
\(\cos x = \frac{{OH}}{{OM}}\)
Đúng 0
Bình luận (0)
a) Xác định điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = 60^\circ \)
b) So sánh hoành độ của điểm M với \(\cos 60^\circ \); tung độ của điểm M với \(\sin 60^\circ \)
a)
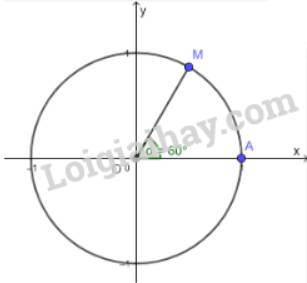
b) \(\cos 60^\circ \) bằng hoành độ của điểm M
\(\sin 60^\circ \) bằng tung độ của điểm M
Đúng 0
Bình luận (0)
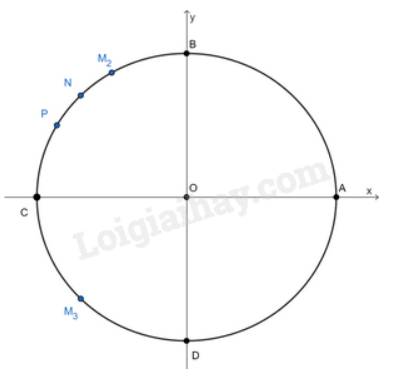
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:
a) \(\frac{{2\pi }}{3}\); b) \( - \frac{{11\pi }}{4}\); c) \({150^0}\); d) \( - {225^0}\).
a) Ta có: \(\frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\). Ta chia đường tròn thành 3 phần bằng nhau. Khi đó điểm \({M_2}\) là điểm biểu diễn bởi góc có số đo \(\frac{{2\pi }}{3}\).
b) Ta có \( - \frac{{11\pi }}{4} = - \frac{{3\pi }}{4} + \left( { - 1} \right).2\pi \). Do đó điểm biểu diễn bởi góc \( - \frac{{11\pi }}{4}\) trùng với góc \( - \frac{{3\pi }}{4}\) và là điểm \({M_3}\).
c) Ta có \(\frac{{150}}{{180}} = \frac{5}{6}\). Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó P là điểm biểu diễn bởi góc \({150^0}\)
d) Ta có \( - {225^0} = - {180^0} - {45^0}\). Do đó điểm biểu diễn N là điểm biểu diễn bởi góc \( - {225^0}\)
Đúng 0
Bình luận (0)
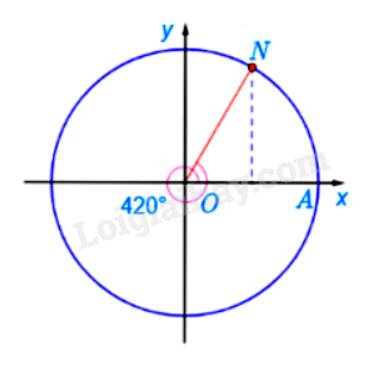
Xác định điểm M và N trên đường tròn lượng giác lần lượt biểu diễn các góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4}\)và \({420^ \circ }\)
Tham khảo:
Điểm biểu diễn góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4} = - \frac{{7\pi }}{4} + ( - 1).2\pi \) được xác định là điểm M.
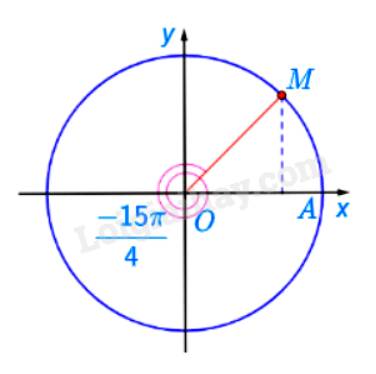
Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)
Đúng 0
Bình luận (0)
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác left( {OA,OM} right) alpha ,,,left( {OA,OM} right) - alpha (Hình 13)a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác alpha ,,v`a ,, - alpha
Đọc tiếp
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác \(\left( {OA,OM} \right) = \alpha ,\,\,\left( {OA,OM'} \right) = - \alpha \) (Hình 13)

a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.
b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)
a) Hoành độ của điểm M và M’ bằng nhau
Tung độ của điểm M và M’ đối nhau
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)

Đúng 0
Bình luận (0)
Trên đường tròn lượng giác góc A lấy điểm M sao cho số đo lượng giác \(\stackrel\frown{AM}\)=\(\alpha\) . Có bao nhiêu điểm M biết \(\alpha=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\left(k\in Z\right)?\)
Cho góc lượng giác có số đo bằng \(\frac{{5\pi }}{6}\)
a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.
b) Tính các giá trị lượng giác của góc lượng giác đã cho.
Tham khảo:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
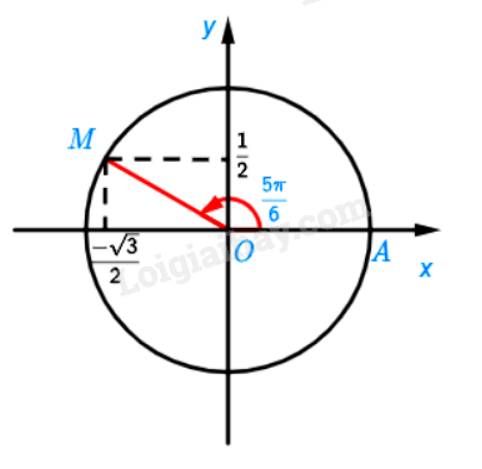
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)
Đúng 0
Bình luận (0)







