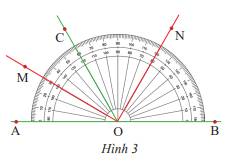
Tìm tia phân giác của các góc: \(\widehat {AOC}\) và \(\widehat {COB}\) trong hình 3.
cho hai góc kề bù \(\widehat{AOC}\)và \(\widehat{COB}\). gọi OM là tia phân giác của \(\widehat{AOC}\). Vẽ tia ON vuông góc với OM tia (OM nằm trong góc \(\widehat{BOC}\)) chứng tở tia ON là tia phân giác của \(\widehat{BOC}\)
Cho \(\widehat{AOB}\)khác góc bẹt, tia OC là tia phân giác của AOB. Các tia OA', OB' VÀ OC' lần lượt là tia đối của các tia OA, OB, OC.
a, Chỉ ra góc đối đỉnh của \(\widehat{AOC;}\widehat{COB}\)
b, Chứng tỏ rằng \(\widehat{A'OC'}\)= \(\widehat{B'OC'}\)
c, Chứng tỏ rằng OC' là tia phân giác của A'OB'
(Thêm hình vẽ giúp mình nhé)
Cho hai góc kề nhau \(\widehat{AOC}\) và \(\widehat{COB}\) sao cho \(\widehat{AOC}\) =\(\frac{3}{4}\)\(\widehat{COB}\) và \(\widehat{AOB}\) =\(^{140^0}\).
a) Tính số đo \(\widehat{AOC}\)VÀ \(\widehat{COB}\)
b) Gọi hai tia OM và ON lần lượt là tua phân giác của \(\widehat{AOC}\)và \(\widehat{COB}\). Tính \(\widehat{MOB}\), \(\widehat{NOA}\), \(\widehat{MON}\)?
c) Vẽ tia OD là tia đối của tia OC. Tính số đo \(\widehat{DOA}\), \(\widehat{DOM}\), \(\widehat{DON}\)?
Cho 2 góc : \(\widehat{AOB}\) và \(\widehat{BOC}\) kề nhau và có tổng = 160 độ . Biết rằng \(\widehat{AOB}-\widehat{AOC}=100^0\)
a ) Tính \(\widehat{AOB}\) và \(\widehat{BOC}\)
b ) Ở miền trong góc AOC vẽ tia OD vuông góc với OC . Tia OD có phải là phân giác của góc BOC không ? Vì sao ?
c ) Vẽ tia OC' là tia đối của tia OC . So sánh góc AOC và góc BOC'
ta co AOB+BOC=160(1)
Va AOB-BOC=100(2)
Cong (1) va (2) ta co
(AOB+BOC)+(AOB-BOC)=160+100
2AOB=260
AOB=130
Lai co AOB+BOC=160
Hay 130+BOC=160
BOC=30
b) Ta co DOB=COD-BOC=60
VA DOA=COA-DOC=60
Vi DOA=DOB va ODnam giua 2 tia OA,OB NEN OD LA TIA phan giac cua AOB
Cho \(\widehat{aOb}\)\(=120^o\).Vẽ tia \(Oc\) trong góc đó sao cho \(\widehat{aOc}\)\(=50^o\).Vẽ tia phân giác \(Om\)của \(\widehat{bOc}\).Tính :
a)Tính \(\widehat{bOm}\)
b)Tính \(\widehat{aOm}\)
a) Trên cùng một nửa mặt phẳng bờ chứa tia Oa, ta có: \(\widehat{aOc}< \widehat{aOb}\left(50^0< 120^0\right)\)
nên tia Oc nằm giữa hai tia Oa và Ob
\(\Leftrightarrow\widehat{aOc}+\widehat{bOc}=\widehat{aOb}\)
\(\Leftrightarrow\widehat{bOc}=\widehat{aOb}-\widehat{aOc}=120^0-50^0=70^0\)
Ta có: Om là tia phân giác của \(\widehat{bOc}\)(gt)
nên \(\widehat{bOm}=\dfrac{\widehat{bOc}}{2}=\dfrac{70^0}{2}\)
hay \(\widehat{bOm}=35^0\)
Vậy: \(\widehat{bOm}=35^0\)
1. Hai đường thẳng AB và CD cắt nhau tại O tạo thành \(\widehat{AOC}\)= 500. Gọi Om là tia phân giác \(\widehat{AOC}\) ; ON là tia đối của tia OM. Tính \(\widehat{BON,}\widehat{DON}\).
2. Cho góc AOB = 50 độ, Oc là tia phân giác của Góc AOB. gọi OD là tia đối của tia OC. trên nửa mặt phẳng bờ CD chứa OA, vẽ tia oa, vẽ tia OE sao cho góc DOE = 25 độ. tìm góc đối đỉnh vs góc DOE
Cho 2 góc kề bù AOC và COB, trong đó COB= 70°. Gọi Ox và Oy làn lượt là tia phân giác của các góc COB và AOC. Từ A kẻ tia Az// Ox cắt tia OC tại điểm E (E khác O). Chứng tỏ EAO=AEO
Ở Hình 31 có góc vuông xOy, các tia On, Oz, Om nằm trong góc đó và \(\widehat {xOn} = \widehat {nOz},\widehat {yOm} = \widehat {mOz}\).
a) Các tia Om, On có tương ứng là tia phân giác của góc yOz và xOz hay không?
b) Cho biết số đo góc mOn.

a) Các tia Om, On tương ứng là tia phân giác của góc yOz và xOz vì:
Tia Om nằm trong góc yOz và \(\widehat {yOm} = \widehat {mOz}\)
Tia On nằm trong góc xOz và \(\widehat {xOn} = \widehat {nOz}\)
b) Vì các tia Om, On tương ứng là tia phân giác của góc yOz và xOz nên: \(\widehat {yOm} = \widehat {mOz} = \frac{1}{2}.\widehat {yOz};\widehat {xOn} = \widehat {nOz} = \frac{1}{2}.\widehat {xOz}\)
Mà tia Oz nằm trong góc xOy nên \(\widehat {yOz} + \widehat {xOz} = \widehat {xOy}\)
\( \Rightarrow \widehat {mOz} + \widehat {zOn} = \frac{1}{2}.\widehat {yOz} + \frac{1}{2}.\widehat {xOz} = \frac{1}{2}.\widehat {xOy}\)
Mà tia Oz nằm trong góc mOn nên \(\widehat {mOz} + \widehat {zOn} = \widehat {mOn}\) và \(\widehat {xOy} = 90^\circ \)
\( \Rightarrow \widehat {mOn} = \frac{1}{2}.90^\circ = 45^\circ \)
Cho hai góc kề nhau AOC và BOC. Gọi OM và ON theo thứ tự là các tia phân giác của các góc AOC và BOC. Giả sử : \(\widehat{AOB}\)= 130 độ> Tính \(\widehat{MON}\).
ta có: OM là tia phân giác góc AOC
=> góc MOC = góc AOC/2
=> góc AOC = góc MOC.2
ta có: ON là tia phân giác góc BOC
=> góc NOC = góc BOC/2
=> góc BOC = góc NOC.2
ta có: hai góc kề nhau AOC và BOC
=> góc AOC + góc BOC = góc AOB
thay số: góc MOC.2 + góc NOC.2 = 130 độ
=> ( góc MOC + góc NOC).2 = 130 độ
góc MOC + góc NOC = 130 độ : 2
góc MOC + góc NOC = 65 độ
mà góc MOC + góc NOC = góc MON ( OC nằm giữa OM,ON)
=> góc MON = 65 độ ( = góc MOC + góc NOC)