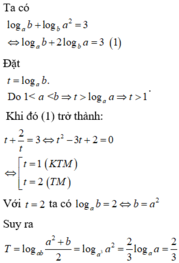cho a,b là 2 số thực phân biệt thỏa mãn a2-3a=b2-3b=1. Tính giá trị của:
a+b ; a2+b2 ; a3+b3 ; a4+b4 ; a5+b5 ; a6+b6

Những câu hỏi liên quan
Cho số thực a, b không âm thỏa mãn a2+b2≤2
Tìm giá trị lớn nhất của biểu thức: C=\(\sqrt{a\left(29a+3b\right)}+\sqrt{b\left(29b+3a\right)}\)
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$C^2\leq (a+b)[(29a+3b)+(29b+3a)]=32(a+b)^2$
$(a+b)^2\leq (a^2+b^2)(1+1)\leq 4$
$\Rightarrow C^2\leq 32.4$
$\Rightarrow C\leq 8\sqrt{2}$
Vậy $C_{\max}=8\sqrt{2}$. Dấu "=" xảy ra khi $a=b=1$
Đúng 3
Bình luận (0)
Cho ba số thực dương a,b,c thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
b
-
6
c
10
và a + c2 . Tính giá trị biểu thức P 3a + 2b + c khi
Q
a
2
+
b...
Đọc tiếp
Cho ba số thực dương a,b,c thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi Q = a 2 + b 2 + c 2 - 14 a - 8 b + 18 c đạt giá trị lớn nhất.
A. 10
B. -10
C. 12
D. -12
Đáp án D

Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất





Đúng 0
Bình luận (0)
Cho hai số thực
a
,
b
phân biệt thỏa mãn
log
3
7
-
3
a
2
-
a
và
log
3
7
-
3
b
2
-
b
Giá trị biểu thứ...
Đọc tiếp
Cho hai số thực a , b phân biệt thỏa mãn log 3 7 - 3 a = 2 - a và log 3 7 - 3 b = 2 - b Giá trị biểu thức 9 a + 9 b bằng
A.67
B.18
C.31
D.82
Cho hai số thực a, b phân biệt thỏa mãn
log
3
7
-
3
a
2
-
α
và
log
3
7
-
3
b
2
-...
Đọc tiếp
Cho hai số thực a, b phân biệt thỏa mãn log 3 7 - 3 a = 2 - α và log 3 7 - 3 b = 2 - b Giá trị biểu thức 9 α + 9 b bằng
A. 67
B. 18
C. 31
D. 82
Cho a, b≥ 0 thỏa mãn: a2+ b2 ≤ 2.
Tìm giá trị lớn nhất của M= a. √(3a(a+2b)) + b. √(3b(b+2a))
Cho a , b là hai số thực dương thỏa mãn
log
5
4
a
+
2
b
+
5
a
+
b
a
+
3
b
-
4
. Tìm giá trị nhỏ nhất của biểu thức
T...
Đọc tiếp
Cho a , b là hai số thực dương thỏa mãn log 5 4 a + 2 b + 5 a + b = a + 3 b - 4 . Tìm giá trị nhỏ nhất của biểu thức T = a 2 + b 2
A. 1 2
B. 1.
C. 3 2
D. 5 2
Ta có:
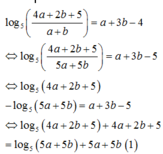
Xét hàm số
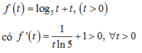
Hàm số f t đồng biến trên 0 ; + ∞
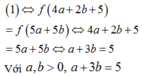
ta có:
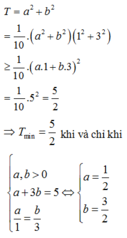
Chọn: D
Đúng 0
Bình luận (0)
Cho a;b là hai số thực dương thỏa mãn
log
5
4
a
+
2
b
+
5
a
+
b
a
+
3
b
−
4
. Tìm giá trị nhỏ nhất của biểu thức
T...
Đọc tiếp
Cho a;b là hai số thực dương thỏa mãn log 5 4 a + 2 b + 5 a + b = a + 3 b − 4 . Tìm giá trị nhỏ nhất của biểu thức T = a 2 + b 2
A. 1/2
B. 5/2
C. 3/2
D. 1
Đáp án B
Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4
⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b
Xét hàm số f t = log 5 t + t t > 0 ⇒ f t đồng biến trên 0 ; + ∞
Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b
⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2
Đúng 0
Bình luận (0)
Cho a, b là 2 số thực phân biệt thỏa mãn a2+4a=b2+4b=1. CMR
a, a+b=-4
b,a3+b3=-76
c, a4+b4=322
a: \(a^2+4a=b^2+4b+1\)
=>\(a^2+4a-b^2-4b=0\)
=>(a-b)(a+b)+4(a-b)=0
=>(a-b)(a+b+4)=0
mà a-b<>0
nên a+b+4=0
=>a+b=-4
b: Đặt \(X=a^3+b^3\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)\)
\(=\left(-4\right)^3-3ab\cdot\left(-4\right)=-64+12ab\)
\(a^2+4a=1\)
=>\(a^2+4a-1=0\)
=>\(a^2+4a+4-5=0\)
=>\(\left(a+2\right)^2=5\)
=>\(\left[\begin{array}{l}a+2=\sqrt5\\ a+2=-\sqrt5\end{array}\right.\Rightarrow\left[\begin{array}{l}a=\sqrt5-2\\ a=-\sqrt5-2\end{array}\right.\)
\(b^2+4b=1\)
=>\(b^2+4b-1=0\)
=>\(b^2+4b+4-5=0\)
=>\(\left(b+2\right)^2=5\)
=>\(\left[\begin{array}{l}b+2=\sqrt5\\ b+2=-\sqrt5\end{array}\right.\Rightarrow\left[\begin{array}{l}b=\sqrt5-2\\ b=-\sqrt5-2\end{array}\right.\)
Vì a<>b nên sẽ có hai trường hợp sau:
TH1: \(a=\sqrt5-2;b=-\sqrt5-2\)
=>\(ab=\left(\sqrt5-2\right)\left(-\sqrt5-2\right)=-\left(\sqrt5-2\right)\left(\sqrt5+2\right)=-1\)
X=-64+12ab
=-64-12
=-76
TH2: \(a=-\sqrt5-2;b=\sqrt5-2\)
=>\(ab=\left(\sqrt5-2\right)\left(-\sqrt5-2\right)=-\left(\sqrt5-2\right)\left(\sqrt5+2\right)=-1\)
X=-64+12ab
=-64-12
=-76
Vậy: X=-76
c: Đặt \(Y=a^4+b^4\)
\(=\left(a^2+b^2\right)^2-2a^2b^2\)
\(=\left\lbrack\left(a+b\right)^2-2ab\right\rbrack^2-2\cdot\left(ab\right)^2\)
\(=\left\lbrack\left(-4\right)^2-2\cdot\left(-1\right)\right\rbrack^2-2\cdot\left(-1\right)^2=\left\lbrack16+2\right\rbrack^2-2\)
\(=18^2-2\)
=324-2
=322
Đúng 0
Bình luận (0)
Cho các số thực a, b thỏa mãn 1 a b và
log
a
b
+
log
b
a
2
3
. Tính giá trị của biểu thức
T
log
a
b
a
2
+
b
2
A.
1...
Đọc tiếp
Cho các số thực a, b thỏa mãn 1< a < b và log a b + log b a 2 = 3 . Tính giá trị của biểu thức T = log a b a 2 + b 2
A. 1 6
B. 3 2
C. 6
D. 2 3