Các câu hỏi tương tự
cho hai số a,b là hai số thực đều lớn hơn 1. giá trị nhỏ nhất của biểu thức s=
\(\dfrac{1}{log_{b\sqrt[3]{a}}}\)+\(\dfrac{1}{log\sqrt[3]{ab^2}}\)
Cho hai số thực
a
,
b
phân biệt thỏa mãn
log
3
7
-
3
a
2
-
a
và
log
3
7
-
3
b
2
-
b
Giá trị biểu thứ...
Đọc tiếp
Cho hai số thực a , b phân biệt thỏa mãn log 3 7 - 3 a = 2 - a và log 3 7 - 3 b = 2 - b Giá trị biểu thức 9 a + 9 b bằng
A.67
B.18
C.31
D.82
Giả sử a, b là các số thực sao cho x3 + y3 a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) z và log(x2 + y2) z + 1. Giá trị của a+b bằng: A.
-
31
2
B.
-
25
2
C.
31
2
D.
29
2
Đọc tiếp
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Cho hai số thực a,b thỏa mãn đồng thời các đẳng thức
3
-
a
.
2
b
1152
và
log
5
a
+
b
2
. Tính giá trị biểu thức
P
a
-
b
A. -3 B. -9 C. 8 D. -6
Đọc tiếp
Cho hai số thực a,b thỏa mãn đồng thời các đẳng thức 3 - a . 2 b = 1152 và log 5 a + b = 2 . Tính giá trị biểu thức P = a - b
A. -3
B. -9
C. 8
D. -6
Cho các số thực dương a,b thỏa mãn
log
a
x
,
log
b
y
. Tính
P
log
(
a
2
b
3
)
Đọc tiếp
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho ba điểm A (0;2;-2), B (-3;1;-1), C (3;-1;2). Điểm M (a;b;c) thuộc mặt phẳng (
α
): 2x -y +2z + 7 0 sao cho biểu thức
3
M
A
→
+
5
M
C
→
-
7
M
C...
Đọc tiếp
Trong không gian Oxyz cho ba điểm A (0;2;-2),
B (-3;1;-1), C (3;-1;2). Điểm M (a;b;c) thuộc
mặt phẳng ( α ): 2x -y +2z + 7 = 0 sao cho biểu
thức 3 M A → + 5 M C → - 7 M C → đạt giá trị nhỏ nhất.
Tính a+b+c
![]()
![]()
![]()
![]()
Cho a, b, c, d, e, f là các số thực thỏa mãn
(
d
-
1
)
2
+
e
-
2
2...
Đọc tiếp
Cho a, b, c, d, e, f là các số thực thỏa mãn
( d - 1 ) 2 + e - 2 2 + f - 3 2 = 1 a + 3 2 + b - 2 2 + c 2 = 9
Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F = a - d 2 + b - e 2 + c - f 2 lần lượt là M, m
Khi đó, M - m bằng:
A. 10
B. 10
C. 8
D. 2 2
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
Cho các số thực a, b thỏa mãn
1
a
b
và
log
a
b
+
log
b
a
2
3
. Tính giá trị của biểu thức
log
a
b...
Đọc tiếp
Cho các số thực a, b thỏa mãn 1 < a < b và log a b + log b a 2 = 3 . Tính giá trị của biểu thức log a b a 2 + b 2
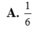
![]()
![]()
![]()






