Các số đo x, y, z trong mỗi tam giác vuông dưới đây bằng bao nhiêu độ?

Tìm tất cả các bộ ba ( x, y, z) sao cho x, y, z là các số nguyên và x, y, z là độ dài ba cạnh của tam giác vuông có số đo diện tích bằng số đo chu vi ( không kể đơn vị đo)
Gọi x; y; z là độ dài ba cạnh tam giác vuông với z là cạnh huyền thì theo đề bài,ta có:
\(z>y\ge x\ge1\) và
\(\hept{\begin{cases}x^2+y^2=z^2\left(\text{Định lí Pythagoras}\right)\\\frac{xy}{2}=x+y+z\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(x+y\right)^2-2xy=z^2\left(1\right)\\xy=2\left(x+y+z\right)\left(2\right)\end{cases}}\)
Thay (2) lên (1) suy ra \(z^2=\left(x+y\right)^2-4\left(x+y+z\right)\)
\(\Leftrightarrow z^2+4z=\left(x+y\right)^2-4\left(x+y\right)\)
\(\Leftrightarrow z^2+4z+4=\left(x+y\right)^2-4\left(x+y\right)+4\)
\(\Leftrightarrow\left(z+2\right)^2=\left(x+y-2\right)^2\) (*)
Do \(z>y\ge x\ge1\) nên cả hai vế cùng không âm.
Do đó từ (*) suy ra \(z+2=x+y-2\Leftrightarrow z=x+y-4\)
Thay ngược lên (2) và giải tiếp bằng cách phân tích đa thức thành nhân tử và lập bảng xét ước:P.
Note: Em không chắc đâu ạ!
Tại sao xy=2(x+y+z) trong khi đó số đo diện tích lại bằng số đo chu vi ( bài tìm các cạnh của tam giác vuông)
Tính số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.
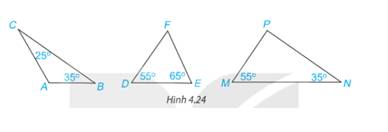
Ta có:
\(\widehat A + \widehat B + \widehat C = {180^o}\)(Định lí tổng 3 góc trong một tam giác)
\(\Rightarrow \widehat A + {25^o} + {35^o} = {180^o} \Rightarrow \widehat A = {180^o}-{25^o} - {35^o}= {120^o}\)
\(\widehat D + \widehat E + \widehat F = {180^o}\)(Định lí tổng 3 góc trong một tam giác)
\(\Rightarrow {55^o} + {65^o} + \widehat F = {180^o} \Rightarrow \widehat F ={180^o}-{55^o} - {65^o}= {60^o}\)
\(\widehat M + \widehat N + \widehat P = {180^o} \)(Định lí tổng 3 góc trong một tam giác)
\(\Rightarrow {55^o} + {35^o} + \widehat P = {180^o} \Rightarrow \widehat P ={180^o}-{55^o} - {35^o}= {90^o}\)
Vậy tam giác MNP vuông tại P.
Tính các số đo x, y trong tam giác dưới đây (H.4.75)
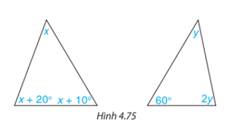
Áp dụng định lí tổng ba góc trong tam giác,
+) Ta có:
\(\begin{array}{l}x + x + {20^o} + x + {10^o} = {180^o}\\ \Rightarrow 3x = {150^o}\\ \Rightarrow x = {50^o}\end{array}\)
+) Ta có:
\(\begin{array}{l}y + {60^o} + 2y = {180^o}\\ \Rightarrow 3y = {120^o}\\ \Rightarrow y = {40^o}\end{array}\)
1, Áp dụng định lý Pytago. Chứng minh rằng nếu ta có a, b, c > 0 sao cho a = m2 + n2 ; b = m2 - n2 ; c = 2mn thì a, b, c là số đo 3 cạnh của tam giác vuông.
2, Các ạnh góc vuông của một tam giác vuông có độ dài a, b và diện tích bằng S. Tính các góc của tam giác vuông đó biết (a + b)2
3, Chứng minh rằng nếu a, b, c là độ dài ba cạnh của 1 tam giác vuông (với a là độ dài cạnh huyền) thì các số x, y, z sau đây cũng là độ dài cạnh của tam giác vuông: x = 9a + 4b +8c ; y = 4a + b+ 4c ; z = 8a + 4b + 7c
Chứng minh rằng nếu a, b, c là số đo của ba cạnh một tam giác vuông với a là độ dài cạnh huyền thì các số x = 9a + 4b + 8c; y = 4a + b + 4c; z = 8a + 4b + 7c cũng là số đo các cạnh của một tam giác vuông khác.
a,b,c là số đo các cạnh của tam giác nên là các số dương, dễ thấy x>y;z
nếu x;y;z là số đo các cạnh của 1 tam giác vuông khác thì x là cạnh huyền
ta xét x2=y2+z2 <=> \(\left(9a+4b+8c\right)^2=\left(4a+b+4c\right)^2+\left(8a+4b+7c\right)^2\)
<=> 81a2+16b2+64c2+72ab+64bc+144ca=80a2+17b2+65c2+72ab+64bc+144ca
<=>a2=b2+c2(đúng do a;b;c là số đo 3 cạnh của 1 tam giác vuông với a độ dài là cạnh huyền,áp dụng định lý Pytago)
Ta đã chứng minh được : x2=y2+z2 .Theo định lý Pytago đảo suy ra x;y;z cũng là số đo 3 cạnh của 1 tam giác vuông
Ta có a,b,c là số đo các cạnh của tam giác nên là các số dương.
Ta thấy x>y;z
Nếu x;y;z là số đo các cạnh của 1 tam giác vuông khác thì x là cạnh huyền
Xét x^2=y^2+z^2 <=>( 9a + 4b + 8c)^2 = (4a + b + 4c)^2+ (8a + 4b + 7c)^2
<=> 81a^2+64c^2+72ab+64bc+144ca=80a^2+17b2^+65c^2+72ab+64bc+144ca
<=>a^2=b^2+c^2
do a;b;c là số đo 3 cạnh của 1 tam giác vuông với a độ dài là cạnh huyền,
Áp dụng định lý Pytago.Ta chứng minh được :
x^2=y^2+z^2
=> x;y;z là số đo 3 cạnh của 1 tam giác vuông (Theo định lý Pytago đảo )
NHỚ TK MK NHA Lưu Đức Mạnh
Lưu Đức Mạnh
Cho biết:
Diện tích của mỗi ô vuông bằng 1cm2 
Mỗi hình tam giác có diện tích bằng 1/2 cm2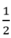
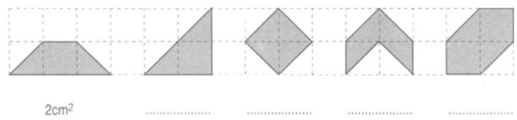
Viết số đo diện tích của mỗi hình dưới đây (theo mẫu):
người ta đặt các khối ô vuông tam giác ô vuông nhỏ lên các đĩa cân như hình dưới đây .Hỏi một khối gỗ tam giác cân nặng bằng bao nhiêu khối gỗ?
Cho tam giác vuông ABC vuông tại A biết góc C = 30 độ và BC= 12cm. Hỏi số đo góc B bằng bao nhiêu độ