Cho hai đường thẳng phân biệt a, b cùng vuông góc với đường thẳng c; d là một đường thẳng khác c và d vuông góc với a. Chứng minh rằng:
a) a // b; b) c // d; c) b\( \bot \)d
Trong các khẳng định sau đây khẳng định nào đúng? khẳng định nào sai?
a) Cho hai đường thẳng a và b song song với nhau. Nếu có một đường thẳng d vuông góc với a thì d vuông góc với b.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.
c) Một mặt phẳng (α) và một đường thẳng a cùng vuông góc với đường thằng b thì a // (α).
d) Hai mặt phẳng (α) và (β) phân biệt cùng vuông góc với một mặt phẳng (γ) thì (α) // (β).
e) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau.
f) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song.
a) Đúng
b) Đúng
c) Sai
d) Sai
e) Sai
f) Đúng
Trong các mệnh đề sau đây, mệnh đề nào là đúng ?
a) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song ;
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song ;
c) Mặt phẳng (α) vuông góc với đường thẳng b và b vuông góc với thẳng a, thì a song song với (α).
d) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song.
e) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song.
a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
e) Sai, chẳng hạn a và b cùng ở trong mp(P) và mp(P) ⊥ d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.
Vẽ ba đường thẳng phân biệt a,b,c sao cho a//b, b//c và hai đường thẳng phân biệt m, n cùng vuông góc với a. Hỏi trên hình có bao nhiêu cặp đường thẳng song song, có bao nhiêu cặp đường thẳng vuông góc?
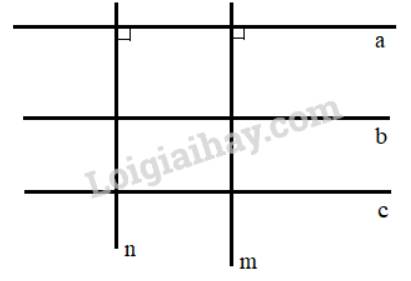
Ta có: +) a // b, b // c nên a // c ( Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau)
+) m \( \bot \) a; n \( \bot \)a nên m // n (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Theo định lý “Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia, ta có:
+) a // b; a \( \bot \)n nên b \( \bot \)n
+) a // b; a \( \bot \)m nên b \( \bot \)m
+) a // c; a \( \bot \)n nên c \( \bot \)n
+) a // c; a \( \bot \)m nên c \( \bot \)m
Vậy các cặp đường thẳng song song là: a // b ; a // c ; b // c; m // n
Các cặp đường thẳng vuôn góc là: b \( \bot \)n; b \( \bot \)m; c \( \bot \)n; c \( \bot \)m; a \( \bot \)n; a \( \bot \)m
Câu 8 : Chọn phát biểu đúng
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng vuông góc với nhau
C. Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng vuông góc với nhau
D. Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng bằng nhau
Câu 9: Điền vào chỗ trống: “Nếu hai đường thẳng d, d' cắt đường thẳng xy tạo thành một cặp góc trong cùng phía .... thì d // d'”
A. Bù nhau
B. Bằng nhau
C. Phụ nhau
D. Kề nhau
Câu 10 : Cho 2 cặp tia đối Ox và Oy; Oz và Ot. Khi đó có bao nhiêu cặp góc đối đỉnh tạo thành?
A.1
B. 2
C.3
D. 4
Câu 11: Cho ![]() đối đỉnh với
đối đỉnh với ![]() và
và ![]() .Tính
.Tính ![]()
A. 300
B. 900
C. 1200
D. 600
Trong các mệnh đề sau đây, mệnh đề nào đúng ?
a) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song sng
c) Mặt phẳng \(\left(\alpha\right)\) vuông góc với đường thẳng b mà b vuông góc với đường thẳng a thì a song song với \(\left(\alpha\right)\)
d) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song
e) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song
a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
Mệnh đề nào sau đây có thể sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song
D. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường thẳng thì song song nhau
Khẳng định nào sau đây là sai? *
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Cho hai đường thẳng a và b song song với nhau, nếu đường thẳng c vuông góc với đường thẳng a thì đường thẳng c cũng vuông góc với đường thẳng b.
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng vuông góc với nhau.
Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Cho hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c tại A và B (Hình 6). Hãy chứng tỏ a // b.
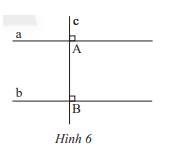
Vì đường thẳng c cắt 2 đường thẳng a, b và tạo thành một cặp góc đồng vị bằng nhau nên a // b (Dấu hiệu nhận biết 2 đường thẳng song song)
Trong các mệnh đề sau đây, mệnh đề nào đúng ? Mệnh đề nào sai ?
a) Cho hai đường thẳng a và b song song với nhau. Nếu có một đường thẳng d vuông góc với a thì d vuông góc với b
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau
c) Một mặt phẳng \(\left(\alpha\right)\) và một đường thẳng a cùng vuông góc với đường thẳng b thì a // \(\left(\alpha\right)\)
d) Hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) phân biệt cùng vuông góc với một mặt phẳng \(\left(\gamma\right)\) thì \(\left(\alpha\right)\) // \(\left(\beta\right)\)
e) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau
f) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song