a)

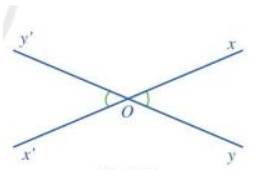
b)

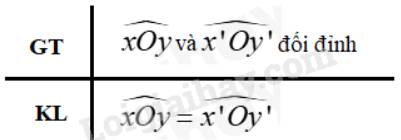
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau

\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù

\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)

\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)

C/m :

Ta có :

\(\begin{cases}\widehat{O_1}+\widehat{O_2}=180^0\\\widehat{O_3}+\widehat{O_2}=180^0\end{cases}\) ( kề bù )

\(\Rightarrow\begin{cases}\widehat{O_1}=180^0-\widehat{O_2}\\\widehat{O_3}=180^0-\widehat{O_2}\end{cases}\)

\(\Rightarrow\widehat{O_1}=\widehat{O_3}\left(đpcm\right)\)

Vì góc O₁ và góc O₂  kề bù => O₁ + O₂ = 180^o

Góc góc O₂ và góc O₃  kề bù => O₂ + O₃ = 180^o

=>  O₁  =  O₂

tham khảo nek bn

a: Giả thiết: a//b

Kết luận: \(\widehat{A_1}=\widehat{B_1}\)

a: 

b: 

Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".

Hình vẽ:

Giả thiết - Kết luận:

Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".

Hình vẽ:

Giả thiết - Kết luận:

A

B

C

O

D

GT:DOA+AOB=90

AOB+BOC=90

KL:DOA=BOC