Cho \(\Delta ABC = \Delta MNP\) và \(\widehat A + \widehat N = 125^\circ \). Tính số đo góc P.

Những câu hỏi liên quan
Cho biết \(\Delta ABC = \Delta MNP\), \(AC = 4\)cm, \(\widehat {MPN} = 45^\circ \). Tính độ dài cạnh MP và số đo góc ACB.
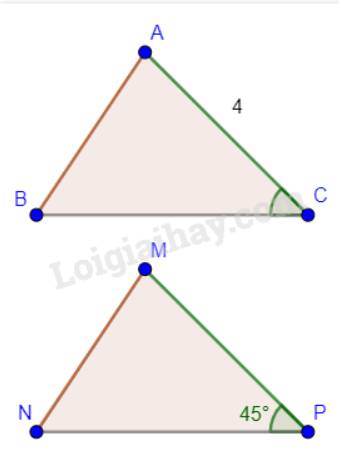
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và MNP thỏa mãn \(\widehat A = 50^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat N = 60^\circ ,\,\,\widehat P = 70^\circ \). Chứng minh \(\Delta ABC \backsim \Delta MNP\).
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)
Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).
Đúng 0
Bình luận (0)
Cho \(\Delta ABC = \Delta DEF\). Biết rằng \(\widehat A = {60^\circ },\hat E = {80^\circ }\), tính số đo các góc B, C, D, F.
Do \(\Delta ABC = \Delta DEF\) nên \(\widehat B = \widehat E = {80^o}\); \(\widehat D = \widehat A = {60^o}\); \(\widehat C = \widehat F\) ( các góc tương ứng)
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 60^\circ + 80^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ - 60^\circ - 80^\circ = 40^\circ \end{array}\)
Do đó \(\widehat F = 40^\circ \)
Vậy \(\widehat B = {80^o}; \widehat D ={60^o}; \widehat C = \widehat F= 40^\circ \).
Đúng 0
Bình luận (0)
Cho biết \(\Delta PQR = \Delta IHK\),\(\widehat P = 71^\circ ,\widehat Q = 49^\circ \). Tính số đo góc K của tam giác IHK.

Ta có: \(\Delta PQR = \Delta IHK\)nên \(\widehat P = \widehat I;\widehat Q = \widehat H;\widehat R = \widehat K\).
\(\Rightarrow \widehat I = 71^\circ ,\widehat H = 49^\circ \). Mà tổng 3 góc trong một tam giác bằng 180° nên trong tam giác IHK:
\(\widehat I + \widehat H + \widehat K = 180^\circ \)
Vậy \(\widehat K = 180^\circ - 71^\circ - 49^\circ = 60^\circ \).
Đúng 0
Bình luận (0)
Cho \(\Delta ABC \backsim \Delta MNP\) và \(\widehat A = 45^\circ ,\,\,\widehat B = 60^\circ \). Tính các góc C, M, N, P.
Vì \(\Delta ABC \backsim \Delta MNP\) nên:
\(\left\{ \begin{array}{l}\widehat A = \widehat M = 45^\circ \\\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P\end{array} \right.\)
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\45^\circ + 60^\circ + \widehat C = 180^\circ \\\widehat C = 180^\circ - 45^\circ - 60^\circ = 75^\circ \end{array}\)
\( \Rightarrow \widehat C = \widehat P = 75^\circ \)
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, \(\widehat A = 65^\circ ,\widehat N = 71^\circ \). Tính số đo các góc còn lại của hai tam giác.

Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Vậy \(\widehat A = \widehat M = 65^\circ \); \(\widehat B = \widehat N = 71^\circ \); \(\widehat C = \widehat P = 180^\circ - 65^\circ - 71^\circ = 44^\circ \)(vì tổng ba góc trong một tam giác bằng 180°).
Đúng 0
Bình luận (0)
Cho Hình 4.20, biết \(AB = CB, AD = CD,\widehat{DAB} = {90^\circ },\widehat{BDC} = {30^\circ }\)
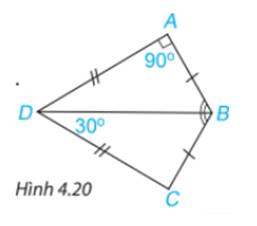
a) Chứng minh rằng \(\Delta ABD = \Delta CBD\).
b) Tính \(\widehat {ABC}\).
a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)
Đúng 0
Bình luận (0)
Cho Delta DEG backsim Delta MNP,,,widehat E 60^circ ,,,widehat M 40^circ .a) Số đo góc D bằng bao nhiêu độ?A. 40^circ B. 50^circ C. 60^circ D. 80^circ b) Số đo góc N bằng bao nhiêu độ?A. 40^circ B. 50^circ C. 60^circ D. 80^circ b) Số đo góc P bằng bao nhiêu độ?A. 40^circ B. 50^circ C. 60^circ D. 80^circ
Đọc tiếp
Cho \(\Delta DEG \backsim \Delta MNP,\,\,\widehat E = 60^\circ ,\,\,\widehat M = 40^\circ \).
a) Số đo góc D bằng bao nhiêu độ?
A. \(40^\circ \)
B. \(50^\circ \)
C. \(60^\circ \)
D. \(80^\circ \)
b) Số đo góc N bằng bao nhiêu độ?
A. \(40^\circ \)
B. \(50^\circ \)
C. \(60^\circ \)
D. \(80^\circ \)
b) Số đo góc P bằng bao nhiêu độ?
A. \(40^\circ \)
B. \(50^\circ \)
C. \(60^\circ \)
D. \(80^\circ \)
a) Vì \(\Delta DEG \backsim \Delta MNP\) nên \(\widehat D = \widehat M,\,\,\widehat E = \widehat N,\,\,\widehat G = \widehat P\)
\( \Rightarrow \widehat D = \widehat M = 40^\circ \)
\( \to \) Chọn đáp án A.
b) Theo câu a) ta có \(\widehat E = \widehat N = 60^\circ \)
\( \to \) Chọn đáp án C.
c) Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\ \Rightarrow 40^\circ + 60^\circ + \widehat P = 180^\circ \\ \Rightarrow \widehat P = 80^\circ \end{array}\)
\( \to \) Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\backsim\Delta DEF\), biết \(\widehat A = 85^\circ ,\widehat B = 60^\circ \). Khi đó số đo \(\widehat F\) bằng
A.\(60^\circ \).
B. \(85^\circ \).
C. \(35^\circ \).
D. \(45^\circ \).
Đáp án đúng là C
Vì \(\Delta ABC\backsim\Delta DEF\) nên \(\widehat A = \widehat D;\widehat B = \widehat E;\widehat C = \widehat F\).
Xét tam giác \(ABC\) có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác).
Thay số, \(85^\circ + 60^\circ + \widehat C = 180^\circ \Rightarrow \widehat C = 180^\circ - 60^\circ - 85^\circ = 35^\circ \)
Vì \(\widehat C = \widehat F\) nên \(\widehat F = 35^\circ \).
Đúng 0
Bình luận (0)







