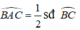Tìm số đo x trong Hình 17
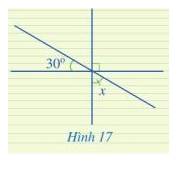
bài 17 cho hình vẽ trên tìm số đo của x
số đo của x
chả lời câu hỏi đi mà
tìm số đo x trong hình bên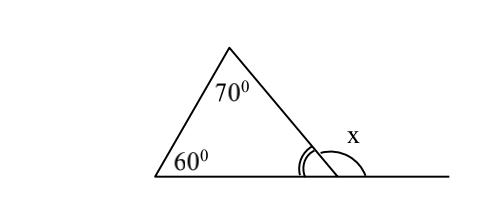
Ta có: △ABC=180o
=> góc C=180o-(70o+60o)=50o
=> C1+C2=180o
=>C2=180o-50o=130o
hay x=130o
Ta chia \(\widehat{x}:\widehat{x1};\widehat{x2}\)
\(\Rightarrow\widehat{x1}=50^o\)
\(\widehat{x1}+\widehat{x2}=180^o\) (kề bù)
\(\Rightarrow\widehat{x2}=180^o-50^o=130^o\)
tìm số đo x trong hình vẽ
Ta có EMN = 1200
MNF = 600
2 góc này ở vị trí trong cùng phía và EMN + MNF = 1200 + 600 = 1800
=> a//b
Mặt khác, EFN = 900
Mà a//b
=> MEF = 900 (từ vuông góc đến song song)
Vì \(\widehat{EMN}+\widehat{MNF}=120^0+60^0=180^0\) mà 2 góc này ở vị trí trong cùng phía nên a//b
Mà \(b\perp EF\) nên \(a\perp EF\)
Do đó \(x=90^0\)
Tìm số đo x trong Hình 115.
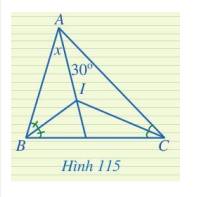
I là giao điểm của hai đường phân giác góc B và góc C.
Vậy I cũng là giao điểm của đường phân giác góc A với góc B và góc C.
Hay AI là phân giác của góc A. Vậy \(x = 30^\circ \).
Tìm số đo x trong hình vẽ sau:
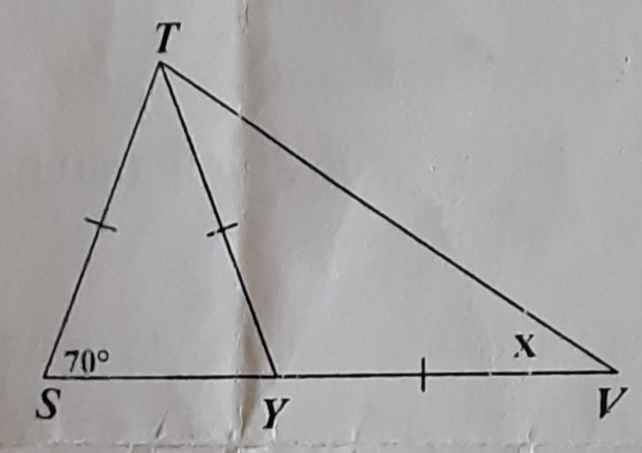
Do tam giác TSY cân tại T \(\Rightarrow\widehat{TSY}=\widehat{TYS}=70^o\)
Mà \(\widehat{TYS}\) là góc ngoài đỉnh Y của tam giác cân TVY
⇒\(2\cdot\widehat{TVY}=\widehat{TYS}=70^o\\ \Rightarrow x=35^o\)
`hat(SYT) = hat(TSY) = 70^o`
`hat(TYV) = 180^o - hat(SYT) = 180^o - 70^o = 110^o`
`=> x = (180^o - 110^o)/2 = 35^o`
Tìm các số đo x, y trong Hình 140.

Tam giác ABO là tam giác đều nên \(\widehat {ABO} = \widehat {AOB} = \widehat {BAO} = 60^\circ \). Vậy \(x = 60^\circ \).
Ba điểm B, O, C thẳng hàng nên \(\widehat {BOC} = 180^\circ \). Mà \(\widehat {AOB} = 60^\circ \)nên \(\widehat {AOC} = 180^\circ - 60^\circ = 120^\circ \).
Xét tam giác AOC có OA = OC. Vậy tam giác AOC cân tại O nên \(\widehat{OAC} = \widehat{OCA} =\dfrac{1}{2}. (180^0-\widehat{AOC})= \dfrac{1}{2}.(180^\circ - 120^\circ ) = 30^\circ \)
Hay \(y = 30^\circ \).
Vậy \(x = 60^\circ \); \(y = 30^\circ \).
Tìm số đo x trong Hình 43, biết u // v
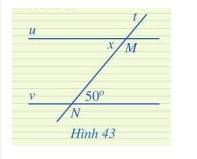
Vì u // v nên x = 50\(^\circ \) ( 2 góc so le trong)
Tìm số đo x của \(\widehat {uOt}\) trong Hình 12.
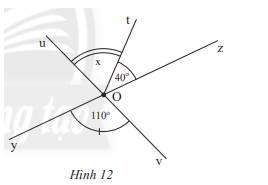
Ta có: \(\widehat {uOz} = \widehat {yOv}\) ( 2 góc đối đỉnh), mà \(\widehat {yOv} = 110^\circ \) nên \(\widehat {uOz} = 110^\circ \)
Mà \(\widehat {uOt},\widehat {tOz}\) là 2 góc kề nhau nên \(\widehat {uOt} + \widehat {tOz} = \widehat {uOz}\)
\(\begin{array}{l} \Rightarrow x + 40^\circ = 110^\circ \\ \Rightarrow x = 110^\circ - 40^\circ = 70^\circ \end{array}\)
Vậy x = 70\(^\circ \)
Bằng dụng cụ, hãy so sánh số đo của góc nội tiếp ∠(BAC) với số đo của cung bị chắn BC trong mỗi hình 16, 17, 18 dưới đây.
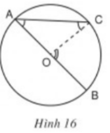

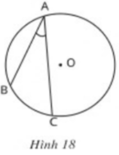
Sử dụng thước đo độ để đo các góc, từ đó ta rút ra kết luận: