a: \(\sqrt{a^2}=\left|a\right|\)

\(\sqrt[3]{a^3}=a\)

b: \(\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}\)

a )

Nếu a + b là số nguyên âm

=> a > b 

b )

Nếu a + b là số nguyên dương :

=> a > b

Vì b < 0 nên dù trong trường hợp nào b cũng âm và a dương 

Số dương đương nhiên lớn hơn số âm

a)    a<b

b)    a>b

thank

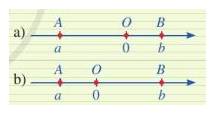
a) Ta có: |a| = OA; |b|  = OB

Vì OA > OB  nên |a| > |b|

b) Ta có: |a| = OA; |b|  = OB

Vì OA < OB  nên |a| < |b|

Chú ý:

Điểm càng xa gốc 0 thì giá trị tuyệt đối của nó càng lớn

|a| = |b|

hoặc |a| > |b|

a) 

\(\overrightarrow a .\overrightarrow b  = ( - 3).2 + 1.6 = 0\)

\( \Rightarrow \overrightarrow a  \bot \overrightarrow b \) hay \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {90^o}\).

b)

\(\left\{ \begin{array}{l}\overrightarrow a .\overrightarrow b  = 3.2 + 1.4 = 10\\|\overrightarrow a |\, = \sqrt {{3^2} + {1^2}}  = \sqrt {10} ;\;\,|\overrightarrow b |\, = \sqrt {{2^2} + {4^2}}  = 2\sqrt 5 \end{array} \right.\)

\(\begin{array}{l} \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{10}}{{\sqrt {10} .2\sqrt 5 }} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {45^o}\end{array}\)

c) Dễ thấy: \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương do \(\frac{{ - \sqrt 2 }}{2} = \frac{1}{{ - \sqrt 2 }}\)

Hơn nữa: \(\overrightarrow b  = \left( {2; - \sqrt 2 } \right) =  - \sqrt 2 .\left( { - \sqrt 2 ;1} \right) =  - \sqrt 2 .\overrightarrow a \;\); \( - \sqrt 2  < 0\)

Do đó: \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng.

\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {180^o}\)

Chú ý:

Khi tính góc, ta kiểm tra các trường hợp dưới đây trước:

+  \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {90^o}\): nếu \(\overrightarrow a .\overrightarrow b  = 0\)

+ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương: 

\(\left( {\overrightarrow a ,\overrightarrow b } \right) = {0^o}\) nếu \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng

\(\left( {\overrightarrow a ,\overrightarrow b } \right) = {180^o}\) nếu \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng

Nếu không thuộc các trường hợp trên thì ta tính góc dựa vào công thức \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).

a)      Ta có: \(2 >  - 5\) nên \(\frac{2}{9} > \frac{{ - 5}}{9}\)hay \(\frac{2}{9} >  - \frac{5}{9}\).

b)      Ta có:

i) \(0 >  - 0,5\) nên  \({0^o}C > - 0,{5^o}C;\)

ii) Do \(12 > 7\) nên \( - 12 <  - 7\). Do đó, \( - {12^o}C < - {7^o}C\).

a)\(3:4\times100=75\%\)

b)\(-2,66:200\times100=-1,33\%\%3\)

c)\(\dfrac{1}{4}:0,5\times100=50\%\)

3:4 x100= 75%

-2,66 : 200 x 100= -1.33%

 1/4 : 0,5 x100 = 50%

a) \(\frac{3}{4} = \left( {\frac{{3.100}}{4}} \right)\%  = 75\% \)

b) \(\frac{{ - 2,66}}{{200}} = \left( {\frac{{ - 2,66.100}}{{200}}} \right)\%  =  - 1,33\% \)

c) \(\frac{{\frac{1}{4}}}{{0,5}} = \left( {\frac{{\frac{1}{4}.100}}{{0,5}}} \right)\%  = 50\% \)