Tính độ dài \(x\) trong Hình 9
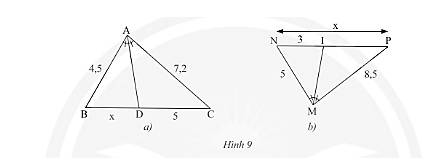
Tính các độ dài \(PN\) và \(BC\) trong Hình 9.
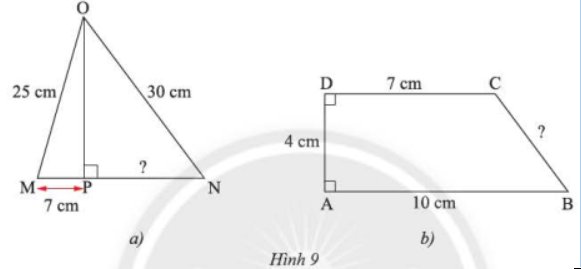
a: QP=căn 25^2-7^2=24cm
PN=căn 30^2-24^2=18cm
b: Kẻ CH vuông góc AB
Xét tứ giác ADCH có
góc ADC=góc A=góc CHA=90 độ
=>ADCH là hcn
=>AH=CD=7cm
=>BH=3cm và CH=AD=4cm
=>BC=căn 3^2+4^2=5cm
Trong Hình 51, biết AB = 4 cm, BC = 7 cm, CD = 3 cm, AD = 9 cm.
a) Tính độ dài đường gấp khúc ABCD.
b) So sánh độ dài đường gấp khúc ABCD và độ dài đoạn thẳng AD.
a)Độ dài đường gấp khúc ABCD là :
AB + BC + CD + AD = 4 + 7 + 3 + 9 = 23 (cm)
b) vì 23 > 9
nên độ dài đường gấp khúc ABCD lớn hơn độ dài đoạn thẳng AD
a) Độ dài đường gấp khúc ABCD là:
4+7+3+9=23(cm)
b) Vì 23cm > 9cm
=> Độ dài đường gấp khúc ABCD lớn hơn độ dài đoạn thẳng AD.
Tính độ dài \(x\) trong Hình 7.

a) Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{CD}}{{BD}} = \frac{{AC}}{{AB}} \Leftrightarrow \frac{x}{{2,4}} = \frac{5}{3} \Rightarrow x = \frac{{2,4.5}}{3} = 4\).
Vậy \(x = 4\).
b) Ta có: \(GH + HF = GF \Rightarrow HF = GF - GH = 20 - x\)
Vì \(EH\) là phân giác của góc \(GEF\) nên theo tính chất đường phân giác ta có:
\(\frac{{GH}}{{HF}} = \frac{{GE}}{{EF}} \Leftrightarrow \frac{x}{{20 - x}} = \frac{{18}}{{12}} \Leftrightarrow \frac{x}{{20 - x}} = \frac{3}{2} \Rightarrow 2x = 3.\left( {20 - x} \right)\)
\( \Leftrightarrow 2x = 60 - 3x \Leftrightarrow 5x = 60 \Rightarrow x = 12\)
Vậy \(x = 12\).
c) Vì \(RS\) là phân giác của góc \(RPQ\) nên theo tính chất đường phân giác ta có:
\(\frac{{PS}}{{SQ}} = \frac{{PR}}{{RQ}} \Leftrightarrow \frac{5}{6} = \frac{{10}}{x} \Rightarrow x = \frac{{10.6}}{5} = 12\).
Vậy \(x = 12\).
a: Xét ΔABC có AD là phân giác
nên CD/AC=BD/AB
=>x/5=2,4/3=4/5
=>x=4
b: Xét ΔEGF có EH là phân giác
nên GH/HF=EG/EF
=>x/20-x=18/12=3/2
=>60-3x=2x
=>x=12
c: Xét ΔRPQ có RS là phân giác
nên PS/SQ=RP/RQ
=>10/x=5/6
=>x=12
Tính độ dài \(x\) trong Hình 8.
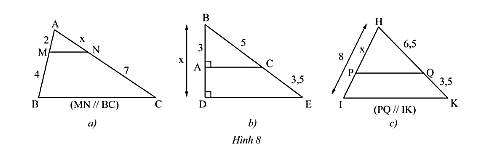
a: Xét ΔABC có MN//BC
nên AN/NC=AM/MB
=>x/7=2/4=1/2
=>x=3,5
b Xét ΔBDE có AC//DE
nên BA/BD=BC/BE
=>3/x=5/8,5=10/17
=>x=51/10
c: Xét ΔHIK có PQ//IK
nên HP/HI=HQ/HK
=>x/8=0,65
=>x=5,2
a) Xét tam giác \(ABC\) ta có \(MN//BC\), theo định lí Thales ta có:
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} \Leftrightarrow \frac{2}{4} = \frac{x}{7} \Rightarrow x = \frac{{2.7}}{4} = 3,5\)
Vậy \(x = 3,5\).
b) Vì \(\left\{ \begin{array}{l}AC \bot BD\\DE \bot BD\end{array} \right. \Rightarrow AC//DE\)
Xét tam giác \(BDE\) ta có \(AC//DE\), theo định lí Thales ta có:
\(\frac{{AB}}{{BD}} = \frac{{BC}}{{BE}} \Leftrightarrow \frac{3}{x} = \frac{5}{{3,5 + 5}} \Rightarrow x = \frac{{3.\left( {3,5 + 5} \right)}}{5} = 5,1\)
Vậy \(x = 5,1\).
c) Xét tam giác \(HIK\) ta có \(PQ//IK\), theo định lí Thales ta có:
\(\frac{{HP}}{{HI}} = \frac{{HQ}}{{HK}} \Leftrightarrow \frac{x}{8} = \frac{{6,5}}{{6,5 + 3,5}} \Rightarrow x = \frac{{8.6,5}}{{\left( {6,5 + 3,5} \right)}} = 5,2\)
Vậy \(x = 5,2\).
Tính độ dài đoạn AE trong hình biết BC//DE và AB=9,BD=3,AC=6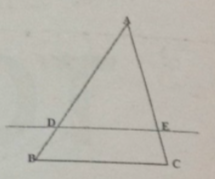
xét tam giác ABC có BC // DE
nên AB/BD = AC/EC
9/3=6/ec=3/1
3EC=6
EC=2
mà AC = EC + AE
6 = 3 + AE
AE = 4
Tính độ dài \(x;y\) trong Hình 8.
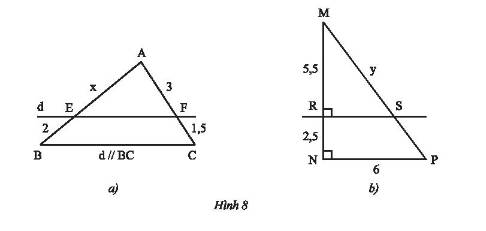
a)
Xét tam giác \(ABC\) có \(d//BC\) mà \(d\) cắt \(AB;AC\) lần lượt tại \(E\) và \(F\)nên theo định lí Thales ta có:
\(\frac{{AE}}{{BE}} = \frac{{AF}}{{CF}} \Rightarrow \frac{x}{2} = \frac{3}{{1,5}}\). Do đó, \(x = \frac{{2.3}}{{1,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MN = NR + MR = 2,5 + 5,5 = 8\)
Xét tam giác \(MNP\) vuông tại \(N\) ta có:
\(M{N^2} + N{P^2} = M{P^2}\)
\({8^2} + {6^2} = M{P^2}\)
\(100 = M{P^2} \Rightarrow MP = \sqrt {100} = 10\)
Xét tam giác \(MNP\) có \(\left\{ \begin{array}{l}RS \bot MN\\NP \bot MN\end{array} \right. \Rightarrow RS//NP\) (quan hệ từ vuông góc đến song song) nên theo định lí Thales ta có:
\(\frac{{MR}}{{MN}} = \frac{{MS}}{{MP}} \Rightarrow \frac{{5,5}}{8} = \frac{y}{{10}}\). Do đó, \(y = \frac{{5,5.10}}{8} = 6,875\).
Vậy \(y = 6,875\).
Tính độ dài x, y trong các hình bên
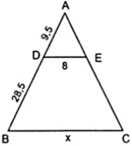
Áp dụng hệ quả của định lí Ta – lét ta có:
DE//BC ⇒ BC/DE = AB/AD hay x/8 = 28,5/9,5
⇔ x = (8.28,5)/9,5 = 456/19 ≈ 31,58
Tính độ dài x, y trong các hình bên
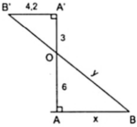
Ta có: A'B'//AB vì cùng vuông góc AA'
Áp dụng hệ quả của định lí Ta – lét ta có:
A'B'//AB ⇒ AB/A'B' = AO/A'O hay x/4,2 = 6/3 ⇔ x = 8,4
Áp dụng định lí Py – ta – go với Δ OAB ta có:
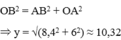
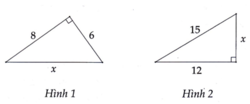
Tính độ dài x trong mỗi hình vẽ sau: