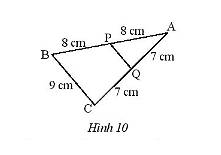
Tính độ dài đoạn \(PQ\) (Hình 10).
Cho đoạn thẳng XY dài 15cm và hai điểm P và Q nằm trong đoạn thẳng đó sao cho XP=PQ=QY. Hãy tính độ dài các đoạn thẳng XP, PQ, QY
Bài 2:Cho hình vuông MNPQ có độ dài PQ = 5cm. Tính độ dài các đoạn MN; NP; QM.
Vì hình vuông có các cạnh bằng nhau nên MN,NP,QM= 5 cm
Bạn tự vẽ hình
Ta có MNPQ là hình vuông
=> MN = NP = QP = MQ = 5cm ( tính chất hình vuông)
Cho tam giác MNP có diện tích là 150cm2 (như hình vẽ). Kéo dài NP một
đoạn PQ có độ dài 6cm thì diện tích tăng 30% diện tích ban đầu. Tính độ dài
đoạn thẳng NP
Độ dài của đoạn thằng NP là :
\(6:30\%=20cm\)
trên tia AM lấy 2 điểm P và Q sao cho AP = 3cm , AQ = 10cm. a) tính độ dài đoạn thẳng PQ b) Gọi điểm I là trung điểm của đoạn PQ. Tính độ dài đoạn thẳng AI
a. Trên nửa mặt phẳng bờ AM ta có AQ = AP + PQ
=> 10cm = 3cm + PQ
=> PQ = 10 - 3
=> PQ = 7cm
b. Ta có I là trung điểm của đoạn PQ
=> PI = QI = PQ : 2
=> PI = QI = 3,5cm
Ta lại có AP + PI = AI
=> 3cm + 3,5cm = AI
=> AI = 6,5cm
Cho biết cạnh mỗi ô vuông bằng \(1cm\). Tính độ dài các đoạn \(PQ,PR,RQ,AB,BC,CA\) trong Hình 11.

Đoạn thẳng \(AB\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{B^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AB = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(AC\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{C^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AC = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(BC\) là đường chéo của hình chữ nhật với chiều dài là \(6cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(B{C^2} = {2^2} + {6^2} = 4 + 36 = 40 \Rightarrow BC = \sqrt {40} = 2\sqrt {10} \)
Từ hình vẽ ta thấy:
\(Q\) là trung điểm của \(AC\);
\(R\) là trung điểm của \(AB\);
\(P\) là trung điểm của \(BC\).
- Vì \(Q\) là trung điểm của \(AC\); \(R\) là trung điểm của \(AB\) nên \(QR\) là đường trung bình của tam giác \(ABC \Rightarrow QR = \frac{1}{2}BC\) (tính chất đường trung bình)
\( \Leftrightarrow QR = \frac{1}{2}.2\sqrt {10} = \sqrt {10} \left( {cm} \right)\).
- Vì \(Q\) là trung điểm của \(AC\); \(P\) là trung điểm của \(BC\) nên \(QP\) là đường trung bình của tam giác \(ABC \Rightarrow QP = \frac{1}{2}AB\) (tính chất đường trung bình)
\( \Leftrightarrow QP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
- \(R\) là trung điểm của \(AB\); \(P\) là trung điểm của \(BC\) nên \(RP\) là đường trung bình của tam giác \(ABC \Rightarrow RP = \frac{1}{2}AC\) (tính chất đường trung bình)
\( \Leftrightarrow RP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
\(AB=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right);AC=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right)\)
BC=căn 2^2+6^2=2*căn 10(cm)
Xét ΔABC có P,Q lần lượt là trung điểm của CB,CA
=>PQ là đường trung bình
=>\(PQ=\dfrac{AB}{2}=\sqrt{5}\left(cm\right)\)
Xét ΔABCcóQ,R lần lượt là trung điểm của AC,AB
=>QR là đường trung bình
=>\(QR=\dfrac{BC}{2}=\sqrt{10}\left(cm\right)\)
Xét ΔABC có P,R lần lượt là trung điểm của BC,BA
=>PR là đường trung bình
=>\(PR=\dfrac{AC}{2}=\sqrt{5}\left(cm\right)\)
cho đoạn thẳng pq dài 12cm gọi e là trung điểm của đoạn thẳng pq và f là trung điểm của đoạn thẳng pe tính độ dài đoạn thẳng pe, ef, và pq giúp em với ạ :
PE=EQ=PQ/2=6(cm)
EF=PF=PE/2=3(cm)
=>PQ=12cm
PE=EQ=PQ/2=6(cm)
EF=PF=PE/2=3(cm)
=>PQ=12cm
Cho hình thang cân PQRS có độ dài đáy PQ là 20 cm, đáy RS ngắn hơn đáy PQ là 12 cm, độ dài cạnh bên PS bằng một nửa độ dài đáy PQ. Tính chu vi hình thang PQRS
Vẽ đoạn thẳng PQ = 8cm. Gọi R là trung điểm của đoạn thẳng PQ.
a) Tính độ dài đoạn RP, RQ.
b) Vẽ S ,T lần lượt là trung điểm của RP ,RQ. Tính độ dài đoạn thẳng ST.
bài 1
cho hình tam abc đều,có độ dài cạnh ab bằng 6 cm.Tính độ dài đoạn tẳng bc và ca
bài 2 cho hình vuông mnpq có độ dài cạnh pq bằng 5cm.Tính độ dài các đoạn thẳng mn,np,qm