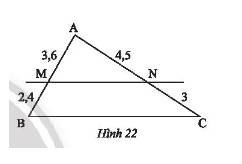
Quan sát Hình 22, chứng minh rằng \(MN//BC\).
Quan sát Hình 10.
a) Tìm đoạn ngắn nhất trong các đoạn BA, BM, BC.
b) Tìm đoạn ngắn nhất trong các đoạn MA, MN, MB.
c) Chứng minh rằng MA < BC.
a) BA là đường vuông góc;
BM và BC là các đường xiên kẻ từ B đến đường thẳng AC
Ta được đường ngắn nhất là đường thẳng vuông góc nên BA là đoạn ngắn nhất.
b) Tương tự câu a
MA là đường vuông góc;
MN và MB là các đường xiên kẻ từ M đến đường thẳng AB
Ta được đường ngắn nhất là đường thẳng vuông góc nên MA là đoạn ngắn nhất.
c) Xét tam giác ABC vuông tại A
\( \Rightarrow \widehat A = {90^o}\)\( \Rightarrow \)A là góc lớn nhất tam giác ABC
\( \Rightarrow \) BC > AC ( định lí về góc đối diện và cạnh )
Vì M nằm giữa AC nên AM < AC
\( \Rightarrow \) AM < AC < BC
Vậy AM < BC
Quan sát Hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC.
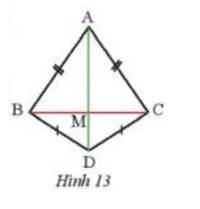
Xét tam giác ABD và tam giác ACD có :
AB = AC ( giả thiết )
BD = CD ( giả thiết )
AD cạnh chung
\( \Rightarrow \Delta ABD =\Delta ACD (c-c-c)\)
\( \Rightarrow \)\(\widehat {BAD} = \widehat {CAD}\)( 2 góc tương ứng )
Xét tam giác ABM và ta giác ACM có :
AB = AC ( giả thiết )
AM cạnh chung
\(\widehat {BAD} = \widehat {CAD}\)( chứng minh trên )
\(\Delta ABM=\Delta ACM (c-g-c)\)
\(\Rightarrow MC = MB\) ( 2 cạnh tương ứng )
\( \Rightarrow \) M là trung điểm BC
Quan sát Hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm. Chứng minh rằng ba điểm A, M, D thẳng hàng.
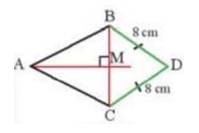
Xét tam giác BCD có BD = CD ( giả thiết )
\( \Rightarrow \) D thuộc trung trực BC do cách đều 2 đầu mút đoạn BC
Mà AM là trung trực của BC
\( \Rightarrow \) D thuộc đường thẳng AM
\( \Rightarrow \) A, M, D thẳng hàng
Quan sát hình 21. Chứng minh rằng tứ giác \(EFGH\) là hình thoi.
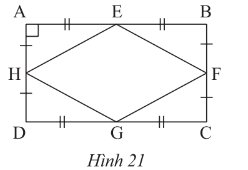
Xét \(\Delta HAE\) và \(\Delta FBE\) ta có:
\(AH = BF\) (gt)
\(\widehat {{\rm{HAE}}} = \widehat {{\rm{FBE}}} = 90^\circ \) (gt)
\(AE = BE\) (gt)
Suy ra \(\Delta HAE = \Delta FBE\) (c-g-c)
Suy ra \(HE = EF\)
Chứng minh tương tự ta có: \(EF = GF\); \(GF = GH\); \(GH = HE\)
Suy ra \(HE = EF = FG = GH\)
Suy ra \(EFGH\) là hình thoi
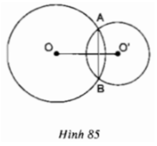
a) Quan sát hình 85, chứng minh rằng OO’ là đường trung trực của AB.
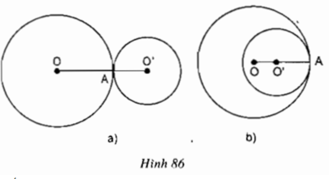
b) Quan sát hình 86, hãy dự đoán về vị trí của điểm A đối với đường nối tâm OO’.
a) Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
b) Hình 86a) Hai đường tròn tiếp xúc ngoài thì A nằm giữa O và O’
Hình 86b) Hai đường tròn tiếp xúc trong thì A nằm ngoài đoạn OO’
Quan sát hình 85, chứng minh rằng OO’ là đường trung trực của AB.
QUẢNG CÁO
Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
Cho hình vẽ dưới đây. Chứng minh rằng MN // CP và M N ⊥ B C
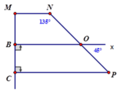
*Ta có B O N ^ = P O x ^ = 45 ° (đối đỉnh) suy ra B O N ^ + O N M ^ = 135 ° + 45 ° = 180 ° mà 2 góc này ở vị trí trong cùng phía nên MN // BO.
* B C ⊥ B O B C ⊥ C P ⇒ B O / / C P ( từ vuông góc đến song song) mà B O / / M N = > ⇒ B O / / M N / / C P (ba đường thẳng song song)
* B C ⊥ C P C P / / M N ⇒ M N ⊥ B C ( từ song song đến vuông góc)
Cho hình bên. Chứng minh rằng MN < BC.
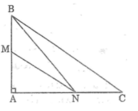
Nối BN.
+ Ta có: AM < AB
Mà NM, NB là các đường xiên ứng với hình chiếu AM, AB
⇒ NM < NB (1)
+ Lại có AN < AC.
Mà BN, BC là các đường xiên ứng với hình chiếu AN, AC
⇒ BN < BC (2)
Từ (1) và (2) suy ra: MN < BC
Quan sát Hình 54, trong đó Cx song song với AB.
a) Tính số đo góc BCx.
b) Chứng minh rằng Cx song song với DE.
c) Tính số đo góc BCD.

a) Vì Cx // AB nên \(\widehat {ABC} = \widehat {BCx}\) ( 2 góc so le trong), mà \(\widehat {ABC} = 45^\circ \Rightarrow \widehat {BCx} = 45^\circ \)
b) Vì AE \( \bot \) AB; AE \( \bot \) ED nên AB // ED (2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
Mà Cx // AB (gt)
\( \Rightarrow \) Cx // ED (2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau)
c) Vì Cx // ED nên \(\widehat {EDC} = \widehat {DCx}\) ( 2 góc so le trong), mà \(\widehat {EDC} = 60^\circ \Rightarrow \widehat {DCx} = 60^\circ \)
Vì tia Cx nằm trong góc BCD nên \(\widehat {BCD} = \widehat {BCx} + \widehat {DCx} = 45^\circ + 60^\circ = 105^\circ \)